均值、中值和众数
从一组数字中我们可以学到什么?
在机器学习(和数学)中,通常存在三中我们感兴趣的值:
- 均值(Mean) - 平均值
- 中值(Median) - 中点值,又称中位数
- 众数(Mode) - 最常见的值
例如:我们已经登记了 13 辆车的速度:
speed = [99,86,87,88,111,86,103,87,94,78,77,85,86]
什么是平均,中间或最常见的速度值?
均值
均值就是平均值。
要计算平均值,请找到所有值的总和,然后将总和除以值的数量:
(99+86+87+88+111+86+103+87+94+78+77+85+86) / 13 = 89.77
NumPy 模块拥有用于此目的的方法:
实例
请使用 NumPy mean() 方法确定平均速度:
import numpy
speed = [99,86,87,88,111,86,103,87,94,78,77,85,86]
x = numpy.mean(speed)
print(x)
中值
中值是对所有值进行排序后的中间值:
77, 78, 85, 86, 86, 86, 87, 87, 88, 94, 99, 103, 111
在找到中位数之前,对数字进行排序很重要。
NumPy 模块拥有用于此目的的方法:
实例
请使用 NumPy median() 方法找到中间值:
import numpy
speed = [99,86,87,88,111,86,103,87,94,78,77,85,86]
x = numpy.median(speed)
print(x)
如果中间有两个数字,则将这些数字之和除以 2。
77, 78, 85, 86, 86, 86, 87, 87, 94, 98, 99, 103
(86 + 87) / 2 = 86.5
实例
使用 NumPy 模块:
import numpy
speed = [99,86,87,88,86,103,87,94,78,77,85,86]
x = numpy.median(speed)
print(x)
众数
众值是出现次数最多的值:
99, 86, 87, 88, 111, 86, 103, 87, 94, 78, 77, 85, 86 = 86
SciPy 模块拥有用于此目的的方法:
实例
请使用 SciPy mode() 方法查找出现次数最多的数字:
from scipy import stats
speed = [99,86,87,88,111,86,103,87,94,78,77,85,86]
x = stats.mode(speed)
print(x)
什么是标准差?
标准差(Standard Deviation,又常称均方差)是一个数字,描述值的离散程度。
低标准偏差表示大多数数字接近均值(平均值)。
高标准偏差表示这些值分布在更宽的范围内。
例如:这次我们已经登记了 7 辆车的速度:
speed = [86,87,88,86,87,85,86]
标准差是:
0.9
意味着大多数值在平均值的 0.9 范围内,即 86.4。
让我们对范围更广的数字集合进行处理:
speed = [32,111,138,28,59,77,97]
标准差是:
37.85
这意味着大多数值都在平均值(平均值为 77.4)的 37.85 范围内。
如您所见,较高的标准偏差表示这些值分布在较宽的范围内。
NumPy 模块有一种计算标准差的方法:
实例
请使用 NumPy std() 方法查找标准差:
import numpy
speed = [86,87,88,86,87,85,86]
x = numpy.std(speed)
print(x)
实例
import numpy
speed = [32,111,138,28,59,77,97]
x = numpy.std(speed)
print(x)
方差
方差是另一种数字,指示值的分散程度。
实际上,如果采用方差的平方根,则会得到标准差!
或反之,如果将标准偏差乘以自身,则会得到方差!
如需计算方差,您必须执行以下操作:
\1. 求均值:
(32+111+138+28+59+77+97) / 7 = 77.4
\2. 对于每个值:找到与平均值的差:
32 - 77.4 = -45.4
111 - 77.4 = 33.6
138 - 77.4 = 60.6
28 - 77.4 = -49.4
59 - 77.4 = -18.4
77 - 77.4 = - 0.4
97 - 77.4 = 19.6
\3. 对于每个差异:找到平方值:
(-45.4)2 = 2061.16
(33.6)2 = 1128.96
(60.6)2 = 3672.36
(-49.4)2 = 2440.36
(-18.4)2 = 338.56
(- 0.4)2 = 0.16
(19.6)2 = 384.16
\4. 方差是这些平方差的平均值:
(2061.16+1128.96+3672.36+2440.36+338.56+0.16+384.16) / 7 = 1432.2
幸运的是,NumPy 有一种计算方差的方法:
实例
使用 NumPy var() 方法确定方差:
import numpy
speed = [32,111,138,28,59,77,97]
x = numpy.var(speed)
print(x)
标准差
如我们所知,计算标准差的公式是方差的平方根:
√1432.25 = 37.85
或者,如上例所示,使用 NumPy 计算标准差:
实例
请使用 NumPy std() 方法查找标准差:
import numpy
speed = [32,111,138,28,59,77,97]
x = numpy.std(speed)
print(x)
符号
标准差通常用 Sigma 符号表示:σ
方差通常由 Sigma Square 符号 σ2 表示
什么是百分位数?
统计学中使用百分位数(Percentiles)为您提供一个数字,该数字描述了给定百分比值小于的值。
例如:假设我们有一个数组,包含住在一条街上的人的年龄。
ages = [5,31,43,48,50,41,7,11,15,39,80,82,32,2,8,6,25,36,27,61,31]
什么是 75 百分位数?答案是 43,这意味着 75% 的人是 43 岁或以下。
NumPy 模块有一种用于找到指定百分位数的方法:
实例
使用 NumPy percentile() 方法查找百分位数:
import numpy
ages = [5,31,43,48,50,41,7,11,15,39,80,82,32,2,8,6,25,36,27,61,31]
x = numpy.percentile(ages, 75)
print(x)
实例
90% 的人口年龄是多少岁?
import numpy
ages = [5,31,43,48,50,41,7,11,15,39,80,82,32,2,8,6,25,36,27,61,31]
x = numpy.percentile(ages, 90)
print(x)
数据分布(Data Distribution)
在本教程稍早之前,我们仅在例子中使用了非常少量的数据,目的是为了了解不同的概念。
在现实世界中,数据集要大得多,但是至少在项目的早期阶段,很难收集现实世界的数据。
我们如何获得大数据集?
为了创建用于测试的大数据集,我们使用 Python 模块 NumPy,该模块附带了许多创建任意大小的随机数据集的方法。
实例
创建一个包含 250 个介于 0 到 5 之间的随机浮点数的数组:
import numpy
x = numpy.random.uniform(0.0, 5.0, 250)
print(x)
直方图
为了可视化数据集,我们可以对收集的数据绘制直方图。
我们将使用 Python 模块 Matplotlib 绘制直方图:
实例
绘制直方图:
import numpy
import matplotlib.pyplot as plt
x = numpy.random.uniform(0.0, 5.0, 250)
plt.hist(x, 5)
plt.show()
结果:
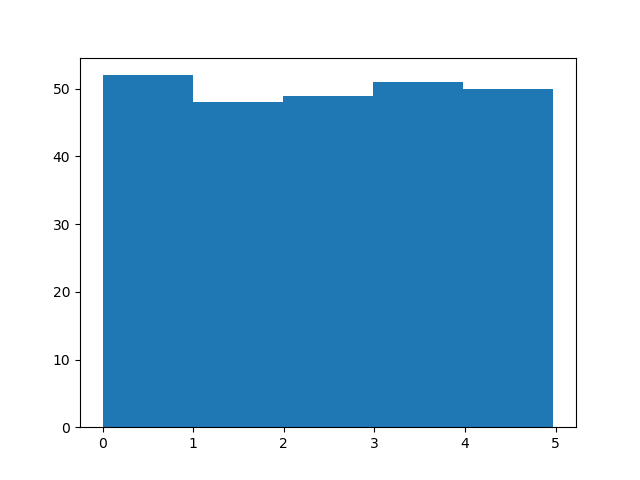
直方图解释
我们使用上例中的数组绘制 5 条柱状图。
第一栏代表数组中有多少 0 到 1 之间的值。
第二栏代表有多少 1 到 2 之间的数值。
等等。
我们得到的结果是:
52 values are between 0 and 1
48 values are between 1 and 2
49 values are between 2 and 3
51 values are between 3 and 4
50 values are between 4 and 5
**注释:**数组值是随机数,不会在您的计算机上显示完全相同的结果。
大数据分布
包含 250 个值的数组被认为不是很大,但是现在您知道了如何创建一个随机值的集,并且通过更改参数,可以创建所需大小的数据集。
实例
创建一个具有 100000 个随机数的数组,并使用具有 100 栏的直方图显示它们:
import numpy
import matplotlib.pyplot as plt
x = numpy.random.uniform(0.0, 5.0, 100000)
plt.hist(x, 100)
plt.show()
正态数据分布(Normal Data Distribution)
在上一章中,我们学习了如何创建给定大小且在两个给定值之间的完全随机数组。
在本章中,我们将学习如何创建一个将值集中在给定值周围的数组。
在概率论中,在数学家卡尔·弗里德里希·高斯(Carl Friedrich Gauss)提出了这种数据分布的公式之后,这种数据分布被称为正态数据分布或高斯数据分布。
实例
典型的正态数据分布:
import numpy
import matplotlib.pyplot as plt
x = numpy.random.normal(5.0, 1.0, 100000)
plt.hist(x, 100)
plt.show()
结果:
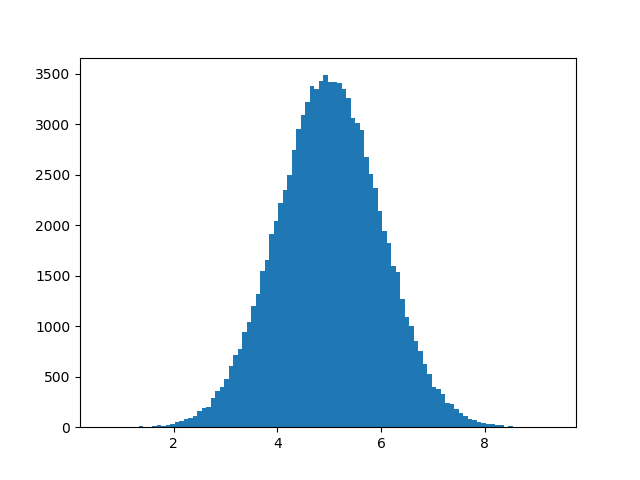
**注释:**由于正态分布图具有钟形的特征形状,因此也称为钟形曲线。
直方图解释
我们使用 numpy.random.normal() 方法创建的数组(具有 100000 个值)绘制具有 100 栏的直方图。
我们指定平均值为 5.0,标准差为 1.0。
这意味着这些值应集中在 5.0 左右,并且很少与平均值偏离 1.0。
从直方图中可以看到,大多数值都在 4.0 到 6.0 之间,最高值大约是 5.0。
散点图(Scatter Plot)
散点图是数据集中的每个值都由点表示的图。
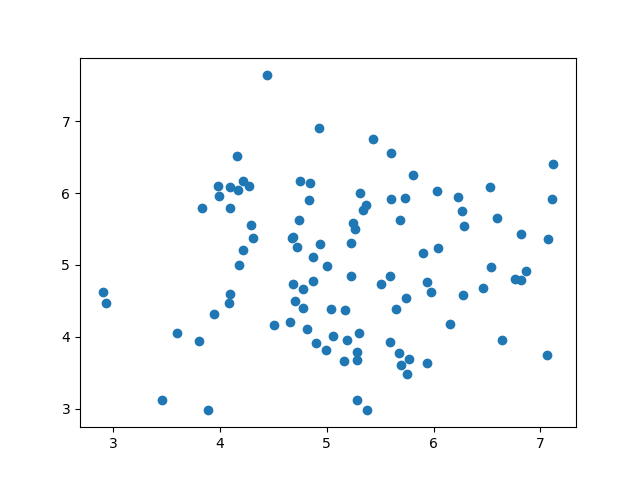
Matplotlib 模块有一种绘制散点图的方法,它需要两个长度相同的数组,一个数组用于 x 轴的值,另一个数组用于 y 轴的值:
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
x 数组代表每辆汽车的年龄。
y 数组表示每个汽车的速度。
实例
请使用 scatter() 方法绘制散点图:
import matplotlib.pyplot as plt
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
plt.scatter(x, y)
plt.show()
结果:
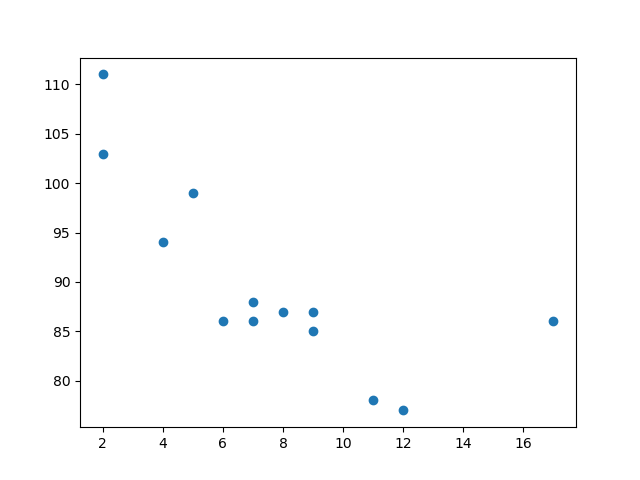
散点图解释
x 轴表示车龄,y 轴表示速度。
从图中可以看到,两辆最快的汽车都使用了 2 年,最慢的汽车使用了 12 年。
**注释:**汽车似乎越新,驾驶速度就越快,但这可能是一个巧合,毕竟我们只注册了 13 辆汽车。
随机数据分布
在机器学习中,数据集可以包含成千上万甚至数百万个值。
测试算法时,您可能没有真实的数据,您可能必须使用随机生成的值。
正如我们在上一章中学到的那样,NumPy 模块可以帮助我们!
让我们创建两个数组,它们都填充有来自正态数据分布的 1000 个随机数。
第一个数组的平均值设置为 5.0,标准差为 1.0。
第二个数组的平均值设置为 10.0,标准差为 2.0:
实例
有 1000 个点的散点图:
import numpy
import matplotlib.pyplot as plt
x = numpy.random.normal(5.0, 1.0, 1000)
y = numpy.random.normal(10.0, 2.0, 1000)
plt.scatter(x, y)
plt.show()
结果:
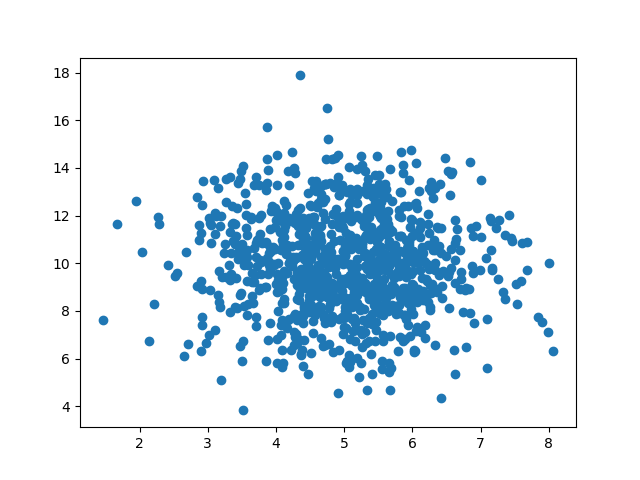
散点图解释
我们可以看到,点集中在 x 轴上的值 5 和 y 轴上的 10 周围。
我们还可以看到,在 y 轴上扩散得比在 x 轴上更大。
回归
当您尝试找到变量之间的关系时,会用到术语“回归”(regression)。
在机器学习和统计建模中,这种关系用于预测未来事件的结果。
线性回归
线性回归使用数据点之间的关系在所有数据点之间画一条直线。
这条线可以用来预测未来的值。
在机器学习中,预测未来非常重要。
工作原理
Python 提供了一些方法来查找数据点之间的关系并绘制线性回归线。我们将向您展示如何使用这些方法而不是通过数学公式。
在下面的示例中,x 轴表示车龄,y 轴表示速度。我们已经记录了 13 辆汽车通过收费站时的车龄和速度。让我们看看我们收集的数据是否可以用于线性回归:
实例
首先绘制散点图:
import matplotlib.pyplot as plt
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
plt.scatter(x, y)
plt.show()
结果:
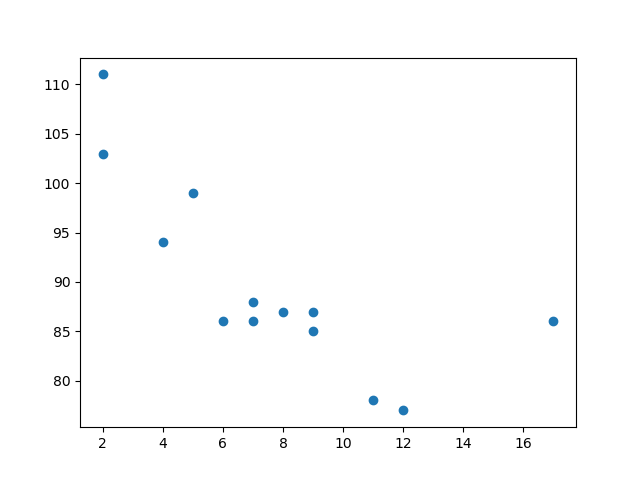
实例
导入 scipy 并绘制线性回归线:
import matplotlib.pyplot as plt
from scipy import stats
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x):
return slope * x + intercept
mymodel = list(map(myfunc, x))
plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()
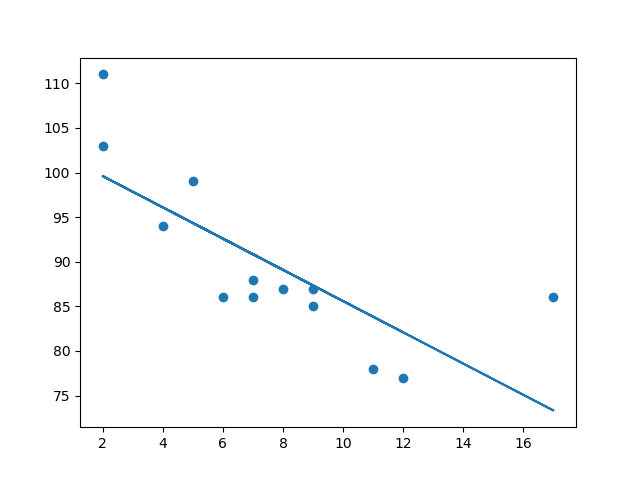
结果:
例子解释
导入所需模块:
import matplotlib.pyplot as plt
from scipy import stats
创建表示 x 和 y 轴值的数组:
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
执行一个方法,该方法返回线性回归的一些重要键值:
slope, intercept, r, p, std_err = stats.linregress(x, y)
创建一个使用 slope 和 intercept 值的函数返回新值。这个新值表示相应的 x 值将在 y 轴上放置的位置:
def myfunc(x):
return slope * x + intercept
通过函数运行 x 数组的每个值。这将产生一个新的数组,其中的 y 轴具有新值:
mymodel = list(map(myfunc, x))
绘制原始散点图:
plt.scatter(x, y)
绘制线性回归线:
plt.plot(x, mymodel)
显示图:
plt.show()
R-Squared
重要的是要知道 x 轴的值和 y 轴的值之间的关系有多好,如果没有关系,则线性回归不能用于预测任何东西。
该关系用一个称为 r 平方(r-squared)的值来度量。
r 平方值的范围是 0 到 1,其中 0 表示不相关,而 1 表示 100% 相关。
Python 和 Scipy 模块将为您计算该值,您所要做的就是将 x 和 y 值提供给它:
实例
我的数据在线性回归中的拟合度如何?
from scipy import stats
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
slope, intercept, r, p, std_err = stats.linregress(x, y)
print(r)
**注释:**结果 -0.76 表明存在某种关系,但不是完美的关系,但它表明我们可以在将来的预测中使用线性回归。
预测未来价值
现在,我们可以使用收集到的信息来预测未来的值。
例如:让我们尝试预测一辆拥有 10 年历史的汽车的速度。
为此,我们需要与上例中相同的 myfunc() 函数:
def myfunc(x):
return slope * x + intercept
实例
预测一辆有 10年车龄的汽车的速度:
from scipy import stats
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x):
return slope * x + intercept
speed = myfunc(10)
print(speed)
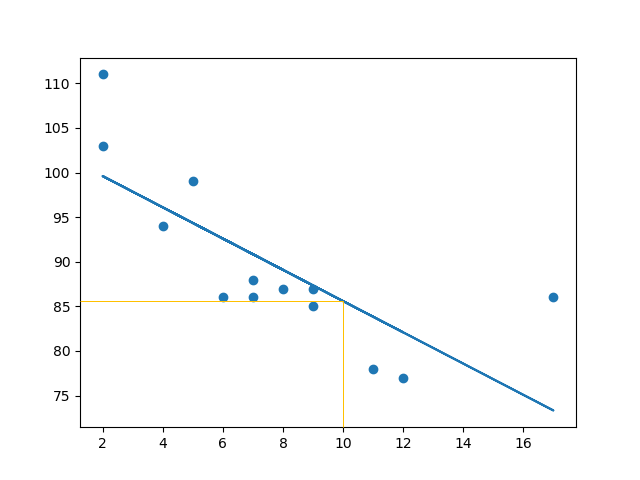
该例预测速度为 85.6,我们也可以从图中读取:
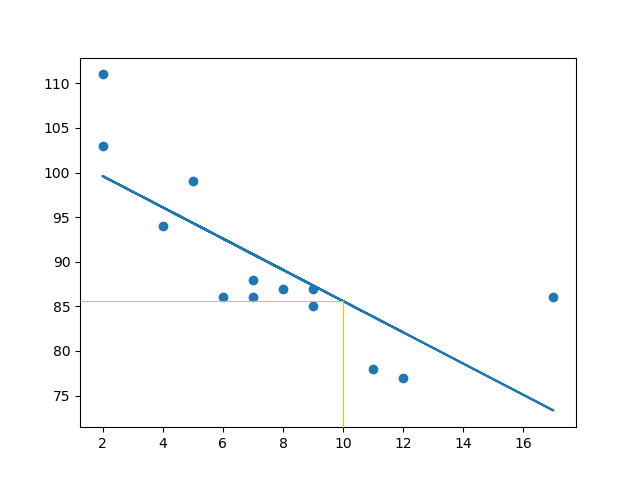
糟糕的拟合度?
让我们创建一个实例,其中的线性回归并不是预测未来值的最佳方法。
实例
x 和 y 轴的这些值将导致线性回归的拟合度非常差:
import matplotlib.pyplot as plt
from scipy import stats
x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x):
return slope * x + intercept
mymodel = list(map(myfunc, x))
plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()
结果:
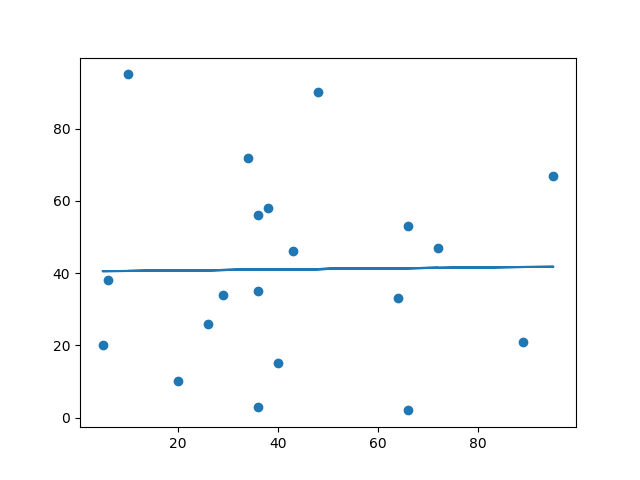
以及 r-squared 值?
实例
您应该得到了一个非常低的 r-squared 值。
import numpy
from scipy import stats
x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]
slope, intercept, r, p, std_err = stats.linregress(x, y)
print(r)
结果:0.013 表示关系很差,并告诉我们该数据集不适合线性回归。
多项式回归(Polynomial Regression)
如果您的数据点显然不适合线性回归(穿过数据点之间的直线),那么多项式回归可能是理想的选择。
像线性回归一样,多项式回归使用变量 x 和 y 之间的关系来找到绘制数据点线的最佳方法。
工作原理
Python 有一些方法可以找到数据点之间的关系并画出多项式回归线。我们将向您展示如何使用这些方法而不是通过数学公式。
在下面的例子中,我们注册了 18 辆经过特定收费站的汽车。
我们已经记录了汽车的速度和通过时间(小时)。
x 轴表示一天中的小时,y 轴表示速度:
实例
首先绘制散点图:
import matplotlib.pyplot as plt
x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]
plt.scatter(x, y)
plt.show()
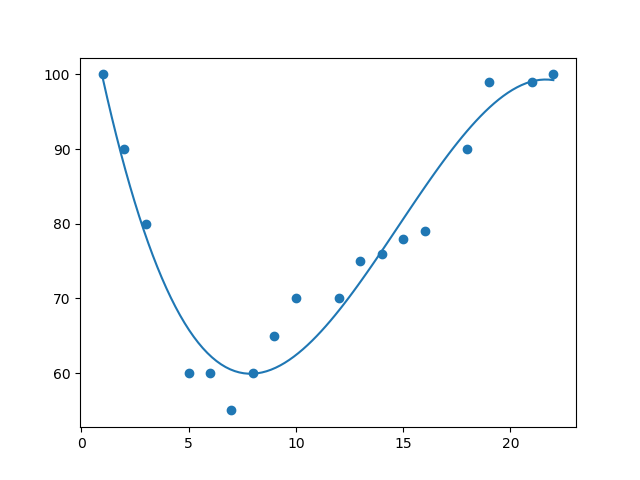
结果:

实例
导入 numpy 和 matplotlib,然后画出多项式回归线:
import numpy
import matplotlib.pyplot as plt
x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]
mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))
myline = numpy.linspace(1, 22, 100)
plt.scatter(x, y)
plt.plot(myline, mymodel(myline))
plt.show()
结果:
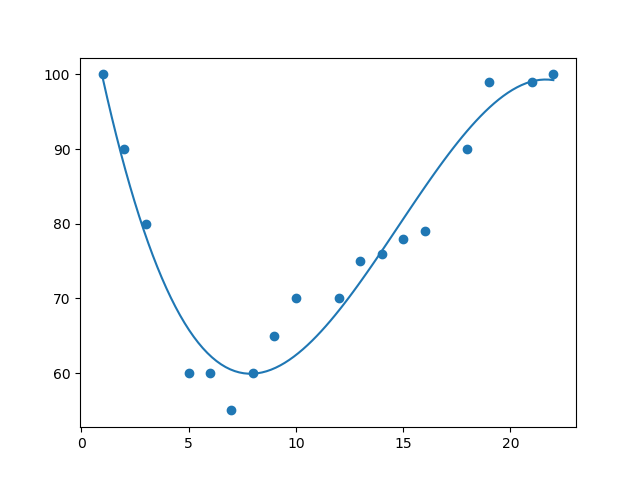
例子解释
导入所需模块:
import numpy
import matplotlib.pyplot as plt
创建表示 x 和 y 轴值的数组:
x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]
NumPy 有一种方法可以让我们建立多项式模型:
mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))
然后指定行的显示方式,我们从位置 1 开始,到位置 22 结束:
myline = numpy.linspace(1, 22, 100)
绘制原始散点图:
plt.scatter(x, y)
画出多项式回归线:
plt.plot(myline, mymodel(myline))
显示图表:
plt.show()
R-Squared
重要的是要知道 x 轴和 y 轴的值之间的关系有多好,如果没有关系,则多项式回归不能用于预测任何东西。
该关系用一个称为 r 平方( r-squared)的值来度量。
r 平方值的范围是 0 到 1,其中 0 表示不相关,而 1 表示 100% 相关。
Python 和 Sklearn 模块将为您计算该值,您所要做的就是将 x 和 y 数组输入:
实例
我的数据在多项式回归中的拟合度如何?
import numpy
from sklearn.metrics import r2_score
x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]
mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))
print(r2_score(y, mymodel(x)))
**注释:**结果 0.94 表明存在很好的关系,我们可以在将来的预测中使用多项式回归。
预测未来值
现在,我们可以使用收集到的信息来预测未来的值。
例如:让我们尝试预测在晚上 17 点左右通过收费站的汽车的速度:
为此,我们需要与上面的实例相同的 mymodel 数组:
mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))
实例
预测下午 17 点过车的速度:
import numpy
from sklearn.metrics import r2_score
x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]
mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))
speed = mymodel(17)
print(speed)
该例预测速度为 88.87,我们也可以在图中看到:

糟糕的拟合度?
让我们创建一个实例,其中多项式回归不是预测未来值的最佳方法。
实例
x 和 y 轴的这些值会导致多项式回归的拟合度非常差:
import numpy
import matplotlib.pyplot as plt
x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]
mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))
myline = numpy.linspace(2, 95, 100)
plt.scatter(x, y)
plt.plot(myline, mymodel(myline))
plt.show()
结果:
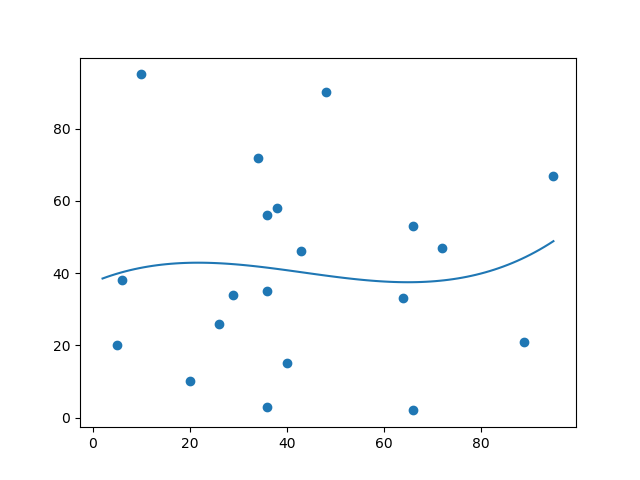
r-squared 值呢?
实例
您应该得到一个非常低的 r-squared 值。
import numpy
from sklearn.metrics import r2_score
x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]
mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))
print(r2_score(y, mymodel(x)))
结果:0.00995 表示关系很差,并告诉我们该数据集不适合多项式回归。
多元回归(Multiple Regression)
多元回归就像线性回归一样,但是具有多个独立值,这意味着我们试图基于两个或多个变量来预测一个值。
请看下面的数据集,其中包含了一些有关汽车的信息。
| Car | Model | Volume | Weight | CO2 |
|---|---|---|---|---|
| Toyota | Aygo | 1000 | 790 | 99 |
| Mitsubishi | Space Star | 1200 | 1160 | 95 |
| Skoda | Citigo | 1000 | 929 | 95 |
| … | … | … | … | … |
我们可以根据发动机排量的大小预测汽车的二氧化碳排放量,但是通过多元回归,我们可以引入更多变量,例如汽车的重量,以使预测更加准确。
工作原理
在 Python 中,我们拥有可以完成这项工作的模块。首先导入 Pandas 模块:
import pandas
Pandas 模块允许我们读取 csv 文件并返回一个 DataFrame 对象。
此文件仅用于测试目的,您可以在此处下载:cars.csv
df = pandas.read_csv("cars.csv")
然后列出独立值,并将这个变量命名为 X。
将相关值放入名为 y 的变量中。
X = df[['Weight', 'Volume']]
y = df['CO2']
**提示:**通常,将独立值列表命名为大写 X,将相关值列表命名为小写 y。
我们将使用 sklearn 模块中的一些方法,因此我们也必须导入该模块:
from sklearn import linear_model
在 sklearn 模块中,我们将使用 LinearRegression() 方法创建一个线性回归对象。
该对象有一个名为 fit() 的方法,该方法将独立值和从属值作为参数,并用描述这种关系的数据填充回归对象:
regr = linear_model.LinearRegression()
regr.fit(X, y)
现在,我们有了一个回归对象,可以根据汽车的重量和排量预测 CO2 值:
# 预测重量为 2300kg、排量为 1300ccm 的汽车的二氧化碳排放量:
predictedCO2 = regr.predict([[2300, 1300]])
实例
请看完整实例:
import pandas
from sklearn import linear_model
df = pandas.read_csv("cars.csv")
X = df[['Weight', 'Volume']]
y = df['CO2']
regr = linear_model.LinearRegression()
regr.fit(X, y)
# 预测重量为 2300kg、排量为 1300ccm 的汽车的二氧化碳排放量:
predictedCO2 = regr.predict([[2300, 1300]])
print(predictedCO2)
结果:
[107.2087328]
我们预测,配备 1.3 升发动机,重量为 2300 千克的汽车,每行驶 1 公里,就会释放约 107 克二氧化碳。
系数
系数是描述与未知变量的关系的因子。
例如:如果 x 是变量,则 2x 是 x 的两倍。x 是未知变量,数字 2 是系数。
在这种情况下,我们可以要求重量相对于 CO2 的系数值,以及体积相对于 CO2 的系数值。我们得到的答案告诉我们,如果我们增加或减少其中一个独立值,将会发生什么。
实例
打印回归对象的系数值:
import pandas
from sklearn import linear_model
df = pandas.read_csv("cars.csv")
X = df[['Weight', 'Volume']]
y = df['CO2']
regr = linear_model.LinearRegression()
regr.fit(X, y)
print(regr.coef_)
结果:
[0.00755095 0.00780526]
结果解释
结果数组表示重量和排量的系数值。
Weight: 0.00755095
Volume: 0.00780526
这些值告诉我们,如果重量增加 1g,则 CO2 排放量将增加 0.00755095g。
如果发动机尺寸(容积)增加 1 ccm,则 CO2 排放量将增加 0.00780526g。
我认为这是一个合理的猜测,但还是请进行测试!
我们已经预言过,如果一辆配备 1300ccm 发动机的汽车重 2300 千克,则二氧化碳排放量将约为 107 克。
如果我们增加 1000g 的重量会怎样?
实例
复制之前的例子,但是将车重从 2300 更改为 3300:
import pandas
from sklearn import linear_model
df = pandas.read_csv("cars.csv")
X = df[['Weight', 'Volume']]
y = df['CO2']
regr = linear_model.LinearRegression()
regr.fit(X, y)
predictedCO2 = regr.predict([[3300, 1300]])
print(predictedCO2)
结果:
[114.75968007]
我们已经预测,配备 1.3 升发动机,重量为 3.3 吨的汽车,每行驶 1 公里,就会释放约 115 克二氧化碳。
这表明 0.00755095 的系数是正确的:
107.2087328 + (1000 * 0.00755095) = 114.75968
特征缩放(Scale Features)
当您的数据拥有不同的值,甚至使用不同的度量单位时,可能很难比较它们。与米相比,公斤是多少?或者海拔比较时间呢?
这个问题的答案是缩放。我们可以将数据缩放为易于比较的新值。
请看下表,它与我们在多元回归一章中使用的数据集相同,但是这次,Volume 列包含的单位是升,而不是 ccm(1.0 而不是 1000)。
很难将排量 1.0 与车重 790 进行比较,但是如果将它们都缩放为可比较的值,我们可以很容易地看到一个值与另一个值相比有多少。
缩放数据有多种方法,在本教程中,我们将使用一种称为标准化(standardization)的方法。
标准化方法使用以下公式:
z = (x - u) / s
其中 z 是新值,x 是原始值,u 是平均值,s 是标准差。
如果从上述数据集中获取 weight 列,则第一个值为 790,缩放后的值为:
(790 - 1292.23) / 238.74 = -2.1
如果从上面的数据集中获取 volume 列,则第一个值为 1.0,缩放后的值为:
(1.0 - 1.61) / 0.38 = -1.59
现在,您可以将 -2.1 与 -1.59 相比较,而不是比较 790 与 1.0。
您不必手动执行此操作,Python sklearn 模块有一个名为 StandardScaler() 的方法,该方法返回带有转换数据集方法的 Scaler 对象。
实例
缩放 Weight 和 Volume 列中的所有值:
import pandas
from sklearn import linear_model
from sklearn.preprocessing import StandardScaler
scale = StandardScaler()
df = pandas.read_csv("cars2.csv")
X = df[['Weight', 'Volume']]
scaledX = scale.fit_transform(X)
print(scaledX)
结果:
请注意,前两个值是 -2.1 和 -1.59,与我们的计算相对应:
[[-2.10389253 -1.59336644]
[-0.55407235 -1.07190106]
...
[ 0.47215993 -0.0289703 ]
[ 0.4302729 2.31762392]]
预测 CO2 值
多元回归一章的任务是在仅知道汽车的重量和排量的情况下预测其排放的二氧化碳。
缩放数据集后,在预测值时必须使用缩放比例:
实例
预测一辆重 2300 公斤的 1.3 升汽车的二氧化碳排放量:
import pandas
from sklearn import linear_model
from sklearn.preprocessing import StandardScaler
scale = StandardScaler()
df = pandas.read_csv("cars2.csv")
X = df[['Weight', 'Volume']]
y = df['CO2']
scaledX = scale.fit_transform(X)
regr = linear_model.LinearRegression()
regr.fit(scaledX, y)
scaled = scale.transform([[2300, 1.3]])
predictedCO2 = regr.predict([scaled[0]])
print(predictedCO2)
结果:
[107.2087328]
评估模型
在机器学习中,我们创建模型来预测某些事件的结果,就像在上一章中当我们了解重量和发动机排量时,预测了汽车的二氧化碳排放量一样。
要衡量模型是否足够好,我们可以使用一种称为训练/测试的方法。
什么是训练/测试
训练/测试是一种测量模型准确性的方法。
之所以称为训练/测试,是因为我们将数据集分为两组:训练集和测试集。
80% 用于训练,20% 用于测试。
您可以使用训练集来训练模型。
您可以使用测试集来测试模型。
训练模型意味着创建模型。
测试模型意味着测试模型的准确性。
从数据集开始
从要测试的数据集开始。
我们的数据集展示了商店中的 100 位顾客及其购物习惯。
实例
import numpy
import matplotlib.pyplot as plt
numpy.random.seed(2)
x = numpy.random.normal(3, 1, 100)
y = numpy.random.normal(150, 40, 100) / x
plt.scatter(x, y)
plt.show()
结果:
x 轴表示购买前的分钟数。
y 轴表示在购买上花费的金额。
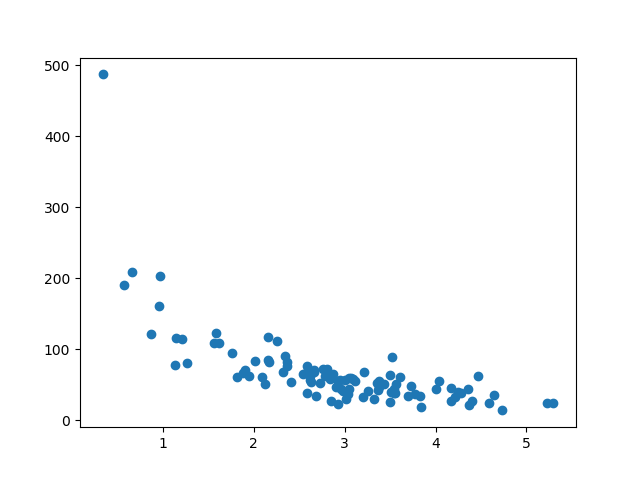
拆分训练/测试
训练集应该是原始数据的 80% 的随机选择。
测试集应该是剩余的 20%。
train_x = x[:80]
train_y = y[:80]
test_x = x[80:]
test_y = y[80:]
显示训练集
显示与训练集相同的散点图:
实例
plt.scatter(train_x, train_y)
plt.show()
结果:
它看起来像原始数据集,因此似乎是一个合理的选择:

显示测试集
为了确保测试集不是完全不同,我们还要看一下测试集。
实例
plt.scatter(test_x, test_y)
plt.show()
结果:
测试集也看起来像原始数据集:
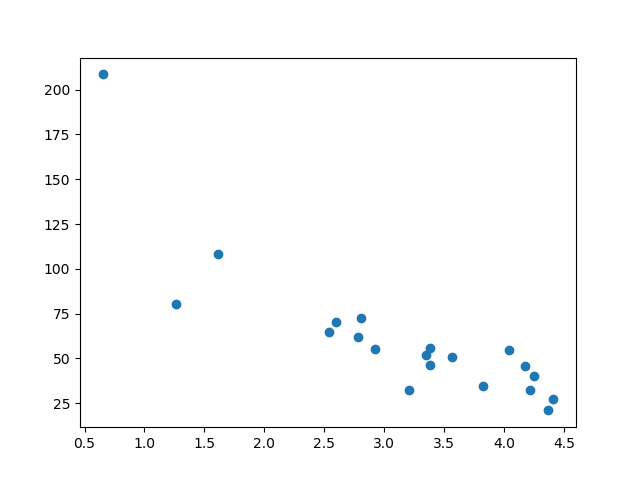
拟合数据集
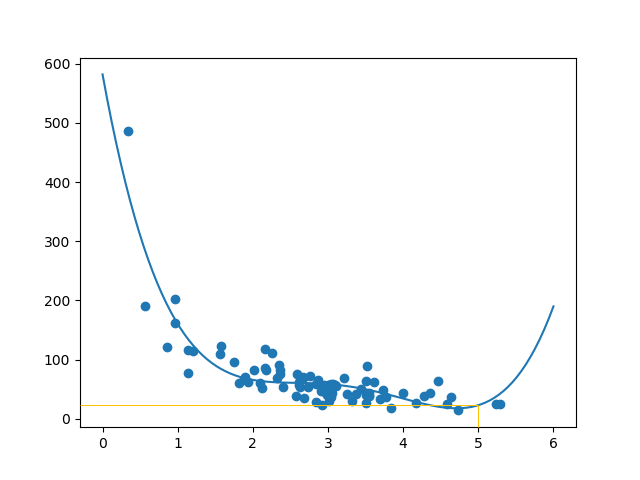
数据集是什么样的?我认为最合适拟合的是多项式回归,因此让我们画一条多项式回归线。
要通过数据点画一条线,我们使用 matplotlib 模块的 plott() 方法:
实例
绘制穿过数据点的多项式回归线:
import numpy
import matplotlib.pyplot as plt
numpy.random.seed(2)
x = numpy.random.normal(3, 1, 100)
y = numpy.random.normal(150, 40, 100) / x
train_x = x[:80]
train_y = y[:80]
test_x = x[80:]
test_y = y[80:]
mymodel = numpy.poly1d(numpy.polyfit(train_x, train_y, 4))
myline = numpy.linspace(0, 6, 100)
plt.scatter(train_x, train_y)
plt.plot(myline, mymodel(myline))
plt.show()
结果:
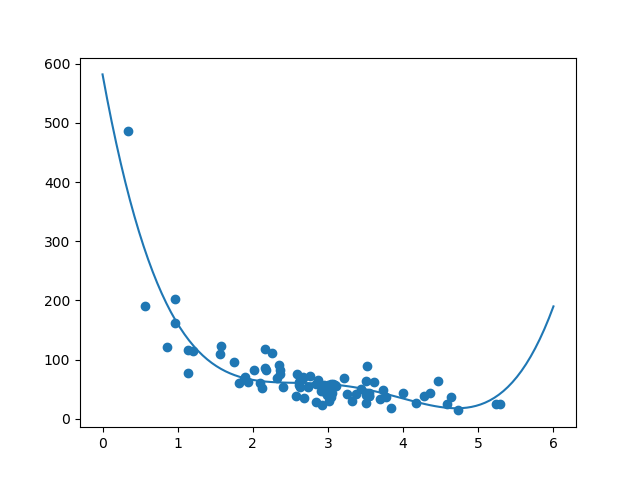
此结果可以支持我们对数据集拟合多项式回归的建议,即使如果我们尝试预测数据集之外的值会给我们带来一些奇怪的结果。例如:该行表明某位顾客在商店购物 6 分钟,会完成一笔价值 200 的购物。这可能是过拟合的迹象。
但是 R-squared 分数呢? R-squared score很好地指示了我的数据集对模型的拟合程度。
R2
还记得 R2,也称为 R平方(R-squared)吗?
它测量 x 轴和 y 轴之间的关系,取值范围从 0 到 1,其中 0 表示没有关系,而 1 表示完全相关。
sklearn 模块有一个名为 rs_score() 的方法,该方法将帮助我们找到这种关系。
在这里,我们要衡量顾客在商店停留的时间与他们花费多少钱之间的关系。
实例
我们的训练数据在多项式回归中的拟合度如何?
import numpy
from sklearn.metrics import r2_score
numpy.random.seed(2)
x = numpy.random.normal(3, 1, 100)
y = numpy.random.normal(150, 40, 100) / x
train_x = x[:80]
train_y = y[:80]
test_x = x[80:]
test_y = y[80:]
mymodel = numpy.poly1d(numpy.polyfit(train_x, train_y, 4))
r2 = r2_score(train_y, mymodel(train_x))
print(r2)
**注释:**结果 0.799 显示关系不错。
引入测试集
现在,至少在训练数据方面,我们已经建立了一个不错的模型。
然后,我们要使用测试数据来测试模型,以检验是否给出相同的结果。
实例
让我们在使用测试数据时确定 R2 分数:
import numpy
from sklearn.metrics import r2_score
numpy.random.seed(2)
x = numpy.random.normal(3, 1, 100)
y = numpy.random.normal(150, 40, 100) / x
train_x = x[:80]
train_y = y[:80]
test_x = x[80:]
test_y = y[80:]
mymodel = numpy.poly1d(numpy.polyfit(train_x, train_y, 4))
r2 = r2_score(test_y, mymodel(test_x))
print(r2)
**注释:**结果 0.809 表明该模型也适合测试集,我们确信可以使用该模型预测未来值。
预测值
现在我们已经确定我们的模型是不错的,可以开始预测新值了。
实例
如果购买客户在商店中停留 5 分钟,他/她将花费多少钱?
print(mymodel(5))
该例预测客户花费了 22.88 美元,似乎与图表相对应:
决策树(Decision Tree)
在本章中,我们将向您展示如何制作“决策树”。决策树是一种流程图,可以帮助您根据以前的经验进行决策。
在这个例子中,一个人将尝试决定他/她是否应该参加喜剧节目。
幸运的是,我们的例中人物每次在镇上举办喜剧节目时都进行注册,并注册一些关于喜剧演员的信息,并且还登记了他/她是否去过。
| Age | Experience | Rank | Nationality | Go |
|---|---|---|---|---|
| 36 | 10 | 9 | UK | NO |
| 42 | 12 | 4 | USA | NO |
| 23 | 4 | 6 | N | NO |
| 52 | 4 | 4 | USA | NO |
| 43 | 21 | 8 | USA | YES |
| 44 | 14 | 5 | UK | NO |
| 66 | 3 | 7 | N | YES |
| 35 | 14 | 9 | UK | YES |
| 52 | 13 | 7 | N | YES |
| 35 | 5 | 9 | N | YES |
| 24 | 3 | 5 | USA | NO |
| 18 | 3 | 7 | UK | YES |
| 45 | 9 | 9 | UK | YES |
现在,基于此数据集,Python 可以创建决策树,这个决策树可用于决定是否值得参加任何新的演出。
工作原理
首先,导入所需的模块,并使用 pandas 读取数据集:
实例
读取并打印数据集:
import pandas
from sklearn import tree
import pydotplus
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
import matplotlib.image as pltimg
df = pandas.read_csv("shows.csv")
print(df)
如需制作决策树,所有数据都必须是数字。
我们必须将非数字列 “Nationality” 和 “Go” 转换为数值。
Pandas 有一个 map() 方法,该方法接受字典,其中包含有关如何转换值的信息。
{‘UK’: 0, ‘USA’: 1, ‘N’: 2}
表示将值 ‘UK’ 转换为 0,将 ‘USA’ 转换为 1,将 ‘N’ 转换为 2。
实例
将字符串值更改为数值:
d = {'UK': 0, 'USA': 1, 'N': 2}
df['Nationality'] = df['Nationality'].map(d)
d = {'YES': 1, 'NO': 0}
df['Go'] = df['Go'].map(d)
print(df)
然后,我们必须将特征列与目标列分开。
特征列是我们尝试从中预测的列,目标列是具有我们尝试预测的值的列。
实例
X 是特征列,y 是目标列:
features = ['Age', 'Experience', 'Rank', 'Nationality']
X = df[features]
y = df['Go']
print(X)
print(y)
现在,我们可以创建实际的决策树,使其适合我们的细节,然后在计算机上保存一个 .png 文件:
实例
创建一个决策树,将其另存为图像,然后显示该图像:
dtree = DecisionTreeClassifier()
dtree = dtree.fit(X, y)
data = tree.export_graphviz(dtree, out_file=None, feature_names=features)
graph = pydotplus.graph_from_dot_data(data)
graph.write_png('mydecisiontree.png')
img=pltimg.imread('mydecisiontree.png')
imgplot = plt.imshow(img)
plt.show()
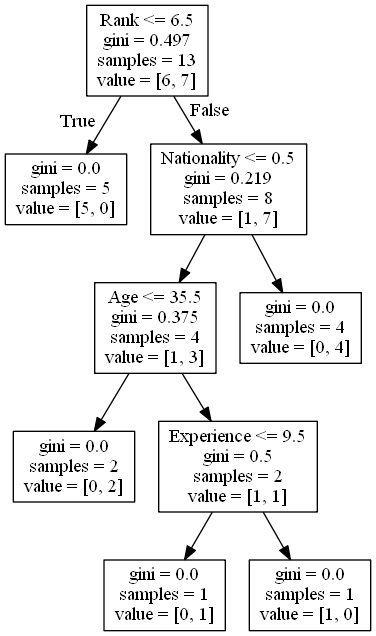
结果解释
决策树使用您先前的决策来计算您是否愿意去看喜剧演员的几率。
让我们阅读决策树的不同方面:

Rank
Rank <= 6.5 表示排名在 6.5 以下的喜剧演员将遵循 True 箭头(向左),其余的则遵循 False 箭头(向右)。
gini = 0.497 表示分割的质量,并且始终是 0.0 到 0.5 之间的数字,其中 0.0 表示所有样本均得到相同的结果,而 0.5 表示分割完全在中间进行。
samples = 13 表示在决策的这一点上还剩下 13 位喜剧演员,因为这是第一步,所以他们全部都是喜剧演员。
value = [6, 7] 表示在这 13 位喜剧演员中,有 6 位将获得 “NO”,而 7 位将获得 “GO”。
Gini
分割样本的方法有很多,我们在本教程中使用 GINI 方法。
基尼方法使用以下公式:
Gini = 1 - (x/n)2 - (y/n)2
其中,x 是肯定答案的数量 (“GO”),n 是样本数量,y 是否定答案的数量 (“NO”),使用以下公式进行计算:
1 - (7 / 13)2 - (6 / 13)2 = 0.497
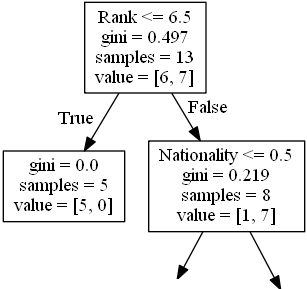
下一步包含两个框,其中一个框用于喜剧演员,其 ‘Rank’ 为 6.5 或更低,其余为一个框。
True - 5 名喜剧演员在这里结束:
gini = 0.0 表示所有样本均得到相同的结果。
samples = 5 表示该分支中还剩下 5 位喜剧演员(5 位的等级为 6.5 或更低的喜剧演员)。
value = [5, 0] 表示 5 得到 “NO” 而 0 得到 “GO”。
False - 8 位戏剧演员继续:
Nationality(国籍)
Nationality <= 0.5 表示国籍值小于 0.5 的喜剧演员将遵循左箭头(这表示来自英国的所有人),其余的将遵循右箭头。
gini = 0.219 意味着大约 22% 的样本将朝一个方向移动。
samples = 8 表示该分支中还剩下 8 个喜剧演员(8 个喜剧演员的等级高于 6.5)。
value = [1, 7] 表示在这 8 位喜剧演员中,1 位将获得 “NO”,而 7 位将获得 “GO”。
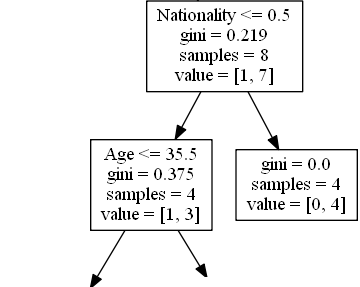
True - 4 名戏剧演员继续:
Age(年龄)
Age <= 35.5 表示年龄在 35.5 岁或以下的喜剧演员将遵循左箭头,其余的将遵循右箭头。
gini = 0.375 意味着大约 37.5% 的样本将朝一个方向移动。
samples = 4 表示该分支中还剩下 4 位喜剧演员(来自英国的 4 位喜剧演员)。
value = [1, 3] 表示在这 4 位喜剧演员中,1 位将获得 “NO”,而 3 位将获得 “GO”。
False - 4 名喜剧演员到这里结束:
gini = 0.0 表示所有样本都得到相同的结果。
samples = 4 表示该分支中还剩下 4 位喜剧演员(来自英国的 4 位喜剧演员)。
value = [0, 4] 表示在这 4 位喜剧演员中,0 将获得 “NO”,而 4 将获得 “GO”。

True - 2 名喜剧演员在这里结束:
gini = 0.0 表示所有样本都得到相同的结果。
samples = 2 表示该分支中还剩下 2 名喜剧演员(2 名 35.5 岁或更年轻的喜剧演员)。
value = [0, 2] 表示在这 2 位喜剧演员中,0 将获得 “NO”,而 2 将获得 “GO”。
False - 2 名戏剧演员继续:
Experience(经验)
Experience <= 9.5 表示具有 9.5 年或以上经验的喜剧演员将遵循左侧的箭头,其余的将遵循右侧的箭头。
gini = 0.5 表示 50% 的样本将朝一个方向移动。
samples = 2 表示此分支中还剩下 2 个喜剧演员(2 个年龄超过 35.5 的喜剧演员)。
value = [1, 1] 表示这两个喜剧演员中,1 将获得 “NO”,而 1 将获得 “GO”。
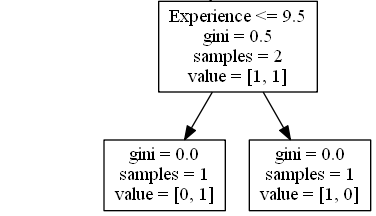
True - 1 名喜剧演员在这里结束:
gini = 0.0 表示所有样本都得到相同的结果。
samples = 1 表示此分支中还剩下 1 名喜剧演员(1 名具有 9.5 年或以下经验的喜剧演员)。
value = [0, 1] 表示 0 表示 “NO”,1 表示 “GO”。
False - 1 名喜剧演员到这里为止:
gini = 0.0 表示所有样本都得到相同的结果。
samples = 1 表示此分支中还剩下 1 位喜剧演员(其中 1 位具有超过 9.5 年经验的喜剧演员)。
value = [1, 0] 表示 1 表示 “NO”,0 表示 “GO”。
预测值
我们可以使用决策树来预测新值。
例如:我是否应该去看一个由 40 岁的美国喜剧演员主演的节目,该喜剧演员有 10 年的经验,喜剧排名为 7?
实例
使用 predict() 方法来预测新值:
print(dtree.predict([[40, 10, 7, 1]]))
实例
如果喜剧等级为 6,答案是什么?
print(dtree.predict([[40, 10, 6, 1]]))
不同的结果
如果运行足够多次,即使您输入的数据相同,决策树也会为您提供不同的结果。
这是因为决策树无法给我们 100% 的肯定答案。它基于结果的可能性,答案会有所不同。
文件处理
在 Python 中使用文件的关键函数是 open() 函数。
open() 函数有两个参数:文件名和模式。
有四种打开文件的不同方法(模式):
- “r” - 读取 - 默认值。打开文件进行读取,如果文件不存在则报错。
- “a” - 追加 - 打开供追加的文件,如果不存在则创建该文件。
- “w” - 写入 - 打开文件进行写入,如果文件不存在则创建该文件。
- “x” - 创建 - 创建指定的文件,如果文件存在则返回错误。
此外,您可以指定文件是应该作为二进制还是文本模式进行处理。
- “t” - 文本 - 默认值。文本模式。
- “b” - 二进制 - 二进制模式(例如图像)。
语法
此外,您可以指定文件是应该作为二进制还是文本模式进行处理:
f = open("demofile.txt")
以上代码等同于:
f = open("demofile.txt", "rt")
因为 “r” (读取)和 “t” (文本)是默认值,所以不需要指定它们。
**注释:**请确保文件存在,否则您将收到错误消息。
在服务器上打开文件
假设我们有以下文件,位于与 Python 相同的文件夹中:
demofile.txt
Hello! Welcome to demofile.txt
This file is for testing purposes.
Good Luck!
如需打开文件,请使用内建的 open() 函数。
open() 函数返回文件对象,此对象有一个 read() 方法用于读取文件的内容:
实例
f = open("demofile.txt", "r")
print(f.read())
只读取文件的一部分
默认情况下,read() 方法返回整个文本,但您也可以指定要返回的字符数:
实例
返回文件中的前五个字符:
f = open("demofile.txt", "r")
print(f.read(5))
读行
您可以使用 readline() 方法返回一行:
实例
读取文件中的一行:
f = open("demofile.txt", "r")
print(f.readline())
通过两次调用 readline(),您可以读取前两行:
实例
读取文件中的两行:
f = open("demofile.txt", "r")
print(f.readline())
print(f.readline())
通过循环遍历文件中的行,您可以逐行读取整个文件:
实例
逐行遍历文件:
f = open("demofile.txt", "r")
for x in f:
print(x)
关闭文件
完成后始终关闭文件是一个好习惯。
实例
完成后关闭文件:
f = open("demofile.txt", "r")
print(f.readline())
f.close()
**注释:**在某些情况下,由于缓冲,您应该始终关闭文件,在关闭文件之前,对文件所做的更改可能不会显示。
写入已有文件
如需写入已有的文件,必须向 open() 函数添加参数:
- “a” - 追加 - 会追加到文件的末尾
- “w” - 写入 - 会覆盖任何已有的内容
实例
打开文件 “demofile2.txt” 并将内容追加到文件中:
f = open("demofile2.txt", "a")
f.write("Now the file has more content!")
f.close()
# 追加后,打开并读取该文件:
f = open("demofile2.txt", "r")
print(f.read())
实例
打开文件 “demofile3.txt” 并覆盖内容:
f = open("demofile3.txt", "w")
f.write("Woops! I have deleted the content!")
f.close()
# 写入后,打开并读取该文件:
f = open("demofile3.txt", "r")
print(f.read())
注释:“w” 方法会覆盖全部内容。
创建新文件
如需在 Python 中创建新文件,请使用 open() 方法,并使用以下参数之一:
- “x” - 创建 - 将创建一个文件,如果文件存在则返回错误
- “a” - 追加 - 如果指定的文件不存在,将创建一个文件
- “w” - 写入 - 如果指定的文件不存在,将创建一个文件
实例
创建名为 “myfile.txt” 的文件:
f = open("myfile.txt", "x")
结果:已创建新的空文件!
实例
如果不存在,则创建新文件:
f = open("myfile.txt", "w")
删除文件
如需删除文件,必须导入 OS 模块,并运行其 os.remove() 函数:
实例
删除文件 “demofile.txt”:
import os
os.remove("demofile.txt")
检查文件是否存在
为避免出现错误,您可能需要在尝试删除文件之前检查该文件是否存在:
实例
检查文件是否存在,然后删除它:
import os
if os.path.exists("demofile.txt"):
os.remove("demofile.txt")
else:
print("The file does not exist")
删除文件
如需删除整个文件夹,请使用 os.rmdir() 方法:
实例
删除文件夹 “myfolder”:
import os
os.rmdir("myfolder")
**提示:**您只能删除空文件夹。
高阶函数
高阶函数英文叫Higher-order function。什么是高阶函数?我们以实际代码为例子,一步一步深入概念。
1. 变量可以指向函数
以Python内置的求绝对值的函数abs()为例,调用该函数用以下代码:
# 调用abs()函数
In [1]: abs(-10)
Out[1]: 10
# 只写abs
In [3]: abs
Out[3]: <function abs>
依据如上例子,可见abs(-10)是对函数的调用,而只写abs是函数本身。
要获得函数调用结果,我们可以把结果赋值给变量:
In [4]: x = abs(-10)
In [5]: x
Out[5]: 10
但是,如果把函数本身赋值给变量呢?
In [6]: fun_abs = abs
In [8]: fun_abs
Out[8]: <function abs>
结论:函数本身也可以赋值给变量,即:变量可以指向函数。
# 变量fun_abs已经指向`abs`函数本身,调用完全和abs一样
In [9]: fun_abs(-10)
Out[9]: 10
2. 传入函数
既然变量可以指向函数,函数的参数能接收变量,那么一个函数就可以接收另一个函数作为参数,这种函数就称之为高阶函数。
一个最简单的高阶函数:
In [10]: def add(x, y, f):
....: return f(x) + f(y)
....:
In [11]: add(-5, -6, abs)
Out[11]: 11
我们将abs函数作为变量传给add()里的f作为高阶函数传参。然后在add里还调用了f的功能。 整个行为流有些像这样:
x = -5
y = -6
f = abs
f(x) + f(y) ==> abs(-5) + abs(6) ==> 11
return 11
把函数作为参数传入,这样的函数称为高阶函数,函数式编程就是指这种高度抽象的编程范式。
map/reduce
Python内建了map()和reduce()函数。
我们先看map。map()函数接收两个参数,一个是函数,一个是Iterable,map将传入的函数依次作用到序列的每个元素,并把结果作为新的Iterator返回。
举例说明,比如我们有一个函数f(x)=x^2,要把这个函数作用在一个list [1, 2, 3, 4, 5, 6, 7, 8, 9]上,就可以用map()实现如下:
In [12]: def f(x):
....: return x * x
....:
In [13]: r = map(f, [1, 2, 3, 4, 5, 6])
In [14]: r
Out[14]: [1, 4, 9, 16, 25, 36]
map()传入的第一个参数是f,即函数对象本身。由于结果r是一个Iterator,Iterator是惰性序列,因此通过list()函数让它把整个序列都计算出来并返回一个list。
然后是reduce()函数。
reduce把一个函数作用在一个序列[x1, x2, x3, ...]上,这个函数必须接收两个参数,reduce把结果继续和序列的下一个元素做累积计算,其效果就是:
reduce(f, [x1, x2, x3, x4]) = f(f(f(x1, x2), x3), x4)
### 计算流像是这个样子
f(x1, x2)
f(f(x1, x2), x3)
f(f(f(x1, x2), x3), x4)
比方说对一个序列求和,就可以用reduce实现:
In [15]: from functools import reduce
In [16]: def add(x, y):
....: return x + y
....:
In [17]: reduce(add, [1, 2, 3, 4, 5])
Out[17]: 15
当然求和运算可以直接用Python内建函数sum(),没必要动用reduce。
但是如果要把序列[1, 3, 5, 7, 9]变换成整数13579,reduce就可以派上用场:
In [18]: from functools import reduce
In [19]: def fn(x, y):
....: return x * 10 + y
....:
In [20]: reduce(fn, [1, 3, 5, 7, 9])
Out[20]: 13579
做个练习,利用map()函数,把用户输入的不规范的英文名字,变为首字母大写,其他小写的规范名字。输入:[‘adam’, ‘LISA’, ‘barT’],输出:[‘Adam’, ‘Lisa’, ‘Bart’]:
"""
第一个版本
"""
# -*- coding: utf-8 -*-
def normalize(name):
return name.upper()[0:1] + name.lower()[1:]
L1 = ['adam', 'LISA', 'barT']
L2 = list(map(normalize, L1))
print(L2)
"""
写完第一个版本后,虽然完成了需求,但是其实有可以优化的地方
觉得下面的写法更pythonic些
"""
# -*- coding: utf-8 -*-
def normalize(name):
this_name = name.lower()
return this_name[0:1].upper() + this_name[1:].lower()
L1 = ['adam', 'LISA', 'barT']
L2 = list(map(normalize, L1))
print(L2)
第二个练习: Python提供的sum()函数可以接受一个list并求和,请编写一个prod()函数,可以接受一个list并利用reduce()求积:
from functools import reduce
def fn(x, y):
return x * y
def prod(L):
return reduce(fn, L)
print("3 * 5 * 7 * 9 =", prod([3, 5, 7, 9]))
练习三:利用map和reduce编写一个str2float函数,把字符串’123.456’转换成浮点数123.456:
# -*- coding: utf-8 -*-
def char2num(s):
return {'0': 0, '1': 1, '2': 2, '3': 3, '4': 4, '5': 5, '6': 6, '7': 7, '8': 8, '9': 9}[s]
def str2int(s):
return reduce(lambda x, y: x * 10 + y, map(char2num, s))
def reduce_float(x, y):
y = 10
return x / y
def return_float(s):
base = 0.1
base_minus = 10
stra = "1"
for i in range(s-1):
stra = stra + '0'
return base / str2int(stra)
def split_float(arg, l_or_r):
if l_or_r == "l":
return arg.split('.')[0]
else:
return arg.split('.')[1]
def str2float(s):
left = split_float(s, "l")
right = split_float(s, "r")
final_left = str2int(left)
r_float = return_float(len(right))
final_right = str2int(right) * r_float
return final_left + final_right
print('str2float(\'123.456\') =', str2float('123.456'))
print('str2float(\'123.888\') =', str2float('123.888'))
filter
Python内建的filter()函数用于过滤序列。
和map()类似,filter()也接收一个函数和一个序列。和map()不同的是,filter()把传入的函数依次作用于每个元素,然后根据返回值是True还是False决定保留还是丢弃该元素。
例如,在一个list中,删掉偶数,只保留奇数,可以这么写:
def is_odd(n):
return n % 2 == 1
list(filter(is_odd, [1,2,3,4,5,6,10,15]))
sorted
排序也是在程序中经常用到的算法。无论使用冒泡排序还是快速排序,排序的核心是比较两个元素的大小。如果是数字,我们可以直接比较,但如果是字符串或者两个dict呢?直接比较数学上的大小是没有意义的,因此,比较的过程必须通过函数抽象出来。
Python内置的sorted()函数就可以对list进行排序:
>>> sorted([36, 5, -12, 9, -21])
[-21, -12, 5, 9, 36]
此外,sorted()函数也是一个高阶函数,它还可以接收一个key函数来实现自定义的排序,例如按绝对值大小排序:
>>> sorted([36, 5, -12, 9, -21], key=abs)
[5, 9, -12, -21, 36]
返回函数
高阶函数除了可以接受函数作为参数外,还可以把函数作为结果值返回。
我们来实现一个可变参数的求和。通常情况下,求和的函数是这样定义的:
def calc_sum(*args):
ax = 0
for n in args:
ax = ax + n
return ax
但是,如果不需要立刻求和,而是在后面的代码中,根据需要再计算怎么办?可以不返回求和的结果,而是返回求和的函数:
def lazy_sum(*args):
def sum():
ax = 0
for n in args:
ax = ax + n
return ax
return sum
当我们调用lazy_sum()时,返回的并不是求和结果,而是求和函数:
>>> f = lazy_sum(1, 3, 5, 7, 9)
>>> f
<function lazy_sum.<locals>.sum at 0x101c6ed90>
调用函数f时,才真正计算求和的结果:
>>> f()
25
在这个例子中,我们在函数lazy_sum中又定义了函数sum,并且,内部函数sum可以引用外部函数lazy_sum的参数和局部变量,当lazy_sum返回函数sum时,相关参数和变量都保存在返回的函数中,这种称为“闭包(Closure)”的程序结构拥有极大的威力。
请再注意一点,当我们调用lazy_sum()时,每次调用都会返回一个新的函数,即使传入相同的参数:
>>> f1 = lazy_sum(1, 3, 5, 7, 9)
>>> f2 = lazy_sum(1, 3, 5, 7, 9)
>>> f1==f2
False
f1()和f2()的调用结果互不影响。
闭包
注意到返回的函数在其定义内部引用了局部变量args,所以,当一个函数返回了一个函数后,其内部的局部变量还被新函数引用,所以,闭包用起来简单,实现起来可不容易。
返回闭包时牢记的一点就是:返回函数不要引用任何循环变量,或者后续会发生变化的变量。
匿名函数 lambda
当我们在传入函数时,有些时候,不需要显式地定义函数,直接传入匿名函数更方便。
在Python中,对匿名函数提供了有限支持。还是以map()函数为例,计算f(x)=x^2时,除了定义一个f(x)的函数外,还可以直接传入匿名函数:
>>> list(map(lambda x: x * x, [1, 2, 3, 4, 5, 6, 7, 8, 9]))
[1, 4, 9, 16, 25, 36, 49, 64, 81]
关键字lambda表示匿名函数,冒号前面的x表示函数参数。
匿名函数有个限制,就是只能有一个表达式,不用写return,返回值就是该表达式的结果。
用匿名函数有个好处,因为函数没有名字,不必担心函数名冲突。此外,匿名函数也是一个函数对象,也可以把匿名函数赋值给一个变量,再利用变量来调用该函数:
>>> f = lambda x: x * x
>>> f
<function <lambda> at 0x101c6ef28>
>>> f(5)
25
同样,也可以把匿名函数作为返回值返回,比如:
def build(x, y):
return lambda: x * x + y * y
Python对匿名函数的支持有限,只有一些简单的情况下可以使用匿名函数。
装饰器
由于函数也是一个对象,而且函数对象可以被赋值给变量,所以,通过变量也能调用该函数。
def now():
print('2016-11-22')
f = now
f()
# 2016-11-22
函数对象有一个__name__属性,可以拿到函数的名字:
>>> now.__name__
'now'
>>> f.__name__
'now'
现在,假设我们要增强now()函数的功能,比如,在函数调用前后自动打印日志,但又不希望修改now()函数的定义,这种在代码运行期间动态增加功能的方式,称之为“装饰器”(Decorator)。
本质上,decorator就是一个返回函数的高阶函数。所以,我们要定义一个能打印日志的decorator,可以定义如下:
def log(func):
def wrapper(*args, **kw):
print('call %s():' % func.__name__)
return func(*args, **kw)
return wrapper
观察上面的log,因为它是一个decorator,所以接受一个函数作为参数,并返回一个函数。我们要借助Python的@语法,把decorator置于函数的定义处:
@log
def now():
print('2015-3-25')
调用now()函数,不仅会运行now()函数本身,还会在运行now()函数前打印一行日志:
>>> now()
call now():
2015-3-25
把@log放到now()函数的定义处,相当于执行了语句:
now = log(now)
由于log()是一个decorator,返回一个函数,所以,原来的now()函数仍然存在,只是现在同名的now变量指向了新的函数,于是调用now()将执行新函数,即在log()函数中返回的wrapper()函数。
wrapper()函数的参数定义是(*args, **kw),因此,wrapper()函数可以接受任意参数的调用。在wrapper()函数内,首先打印日志,再紧接着调用原始函数。
如果decorator本身需要传入参数,那就需要编写一个返回decorator的高阶函数,写出来会更复杂。比如,要自定义log的文本:
def log(text):
def decorator(func):
def wrapper(*args, **kw):
print('%s %s():' % (text, func.__name__))
return func(*args, **kw)
return wrapper
return decorator
这个3层嵌套的decorator用法如下:
@log('execute')
def now():
print('2015-3-25')
偏函数
Python的functools模块提供了很多有用的功能,其中一个就是偏函数(Partial function)。要注意,这里的偏函数和数学意义上的偏函数不一样。
在介绍函数参数的时候,我们讲到,通过设定参数的默认值,可以降低函数调用的难度。而偏函数也可以做到这一点。举例如下:
int()函数可以把字符串转换为整数,当仅传入字符串时,int()函数默认按十进制转换:
>>> int('12345')
12345
但int()函数还提供额外的base参数,默认值为10。如果传入base参数,就可以做N进制的转换:
>>> int('12345', base=8)
5349
>>> int('12345', 16)
74565
假设要转换大量的二进制字符串,每次都传入int(x, base=2)非常麻烦,于是,我们想到,可以定义一个int2()的函数,默认把base=2传进去:
def int2(x, base=2):
return int(x, base)
这样,我们转换二进制就非常方便了:
>>> int2('1000000')
64
>>> int2('1010101')
85
functools.partial就是帮助我们创建一个偏函数的,不需要我们自己定义int2(),可以直接使用下面的代码创建一个新的函数int2:
>>> import functools
>>> int2 = functools.partial(int, base=2)
>>> int2('1000000')
64
>>> int2('1010101')
85
所以,简单总结functools.partial的作用就是,把一个函数的某些参数给固定住(也就是设置默认值),返回一个新的函数,调用这个新函数会更简单。
注意到上面的新的int2函数,仅仅是把base参数重新设定默认值为2,但也可以在函数调用时传入其他值:
>>> int2('1000000', base=10)
1000000
最后,创建偏函数时,实际上可以接收函数对象、*args和**kw这3个参数,当传入:
int2 = functools.partial(int, base=2)
实际上固定了int()函数的关键字参数base,也就是:
int2('10010')
相当于:
kw = { 'base': 2 }
int('10010', **kw)
当函数的参数个数太多,需要简化时,使用functools.partial可以创建一个新的函数,这个新函数可以固定住原函数的部分参数,从而在调用时更简单。
NumPy 数值分析
一、求解线性方程
在本节中,您将学习如何使用linalg.solve()方法求解线性方程。 当您有线性方程要求解时 ,在简单情况下,您只需计算A的反函数即可。然后将其乘以B即可得到解,但是当A具有高维数时,这使得计算起来很难进行计算A的倒数。 让我们从具有三个未知数的三个线性方程式的示例开始,如下所示:
In [44]: A = np.array([[2, 1, 2], [3, 2, 1], [0, 1, 1]])
A
Out[44]: array([[2, 1, 2],
[3, 2, 1],
[0, 1, 1]])
In [45]: B = np.array([8,3,4])
B
Out[45]: array([8, 3, 4])
In [46]: A_inv = np.linalg.inv(A)
A_inv
Out[46]: array([[ 0.2, 0.2, -0.6],
[-0.6, 0.4, 0.8],
[ 0.6, -0.4, 0.2]])
In [47]: np.dot(A_inv,B)
Out[47]: array([-0.2, -0.4, 4.4])
最后,得到a = -0.2,b = -0.4和c = 4.4的结果。 现在,让我们使用linalg.solve()执行相同的计算,如下所示:
In [48]: A = np.array([[2, 1, 2], [3, 2, 1], [0, 1, 1]])
B = np.array([8,3,4])
x = np.linalg.solve(A, B)
x
Out[48]: array([-0.2, -0.4, 4.4])
为了检查我们的结果,我们可以使用allclose()函数,该函数用于按元素比较两个数组:
In [49]: np.allclose(np.dot(A, x), B)
Out[49]: True
linalg.lstsq()方法是求解线性方程组的另一个重要函数,它返回最小二乘解。 此函数将返回回归线的参数。 回归线的主要思想是最小化每个数据点到回归线的距离平方和。 距离的平方和实际上量化了回归线的总误差。 距离越大,误差越大。 因此,我们正在寻找可以最大程度减少此误差的参数。 为了可视化我们的线性回归模型,我们将使用一个非常流行的 Python 二维绘图库matplotlib。 以下代码块在矩阵中运行最小二乘解,并返回权重和偏差:
In [50]: from numpy import arange,array,ones,linalg
from pylab import plot,show
x = np.arange(1,11)
A = np.vstack([x, np.ones(len(x))]).T
A
Out[50]: array([[ 1., 1.],
[ 2., 1.],
[ 3., 1.],
[ 4., 1.],
[ 5., 1.],
[ 6., 1.],
[ 7., 1.],
[ 8., 1.],
[ 9., 1.],
[ 10., 1.]])
In [51]: y = [5, 6, 6.5, 7, 8,9.5, 10, 10.4,13.1,15.5]
w = linalg.lstsq(A,y)[0]
w
Out[51]: array([ 1.05575758, 3.29333333])
In [52]: line = w[0]*x+w[1]
plot(x,line,'r-',x,y,'o')
show()
上图给出了适合我们数据的回归线拟合结果。 该模型生成可用于预测或预测的线性线。 尽管线性回归有很多假设(恒定方差,误差的独立性,线性等),但它仍然是建模数据点之间线性关系的最常用方法。
二、计算梯度
当您有一条直线时,您可以使用导数,以便导数显示该线的斜率。 当函数中有多个变量时,梯度是导数的泛化,因此,梯度的结果实际上是向量函数,而不是导数中的标量值。 ML 的主要目标实际上是找到适合您数据的最佳模型。 您可以通过将损失函数或目标函数最小化来求值最佳均值。 梯度用于查找系数或函数,以最大程度地减少损失或成本函数。 查找最佳点的一种众所周知的方法是采用目标函数的导数,然后将其设置为零以找到模型系数。 如果系数不止一个,则它将成为梯度而不是导数,并且将成为向量方程式而不是标量值。 您可以在每个点上将梯度解释为向量,该梯度将指向函数的下一个局部最小值。 有一种非常流行的优化技术,可以通过计算每个点的梯度并沿该方向移动系数来寻找函数的最小值,以寻求最小值。 该方法称为梯度下降。 在 NumPy 中,gradient()函数用于计算数组的梯度:
In [53]: a = np.array([1,3, 6, 7, 11, 14])
gr = np.gradient(a)
gr
Out[53]: array([ 2\. , 2.5, 2\. , 2.5, 3.5, 3\. ])
让我们看看如何计算此梯度:
gr[0] = (a[1]-a[0])/1 = (3-1)/1 = 2
gr[1] = (a[2]-a[0])/2 = (6-1)/2 = 2.5
gr[2] = (a[3]-a[1])/2 = (7-3)/2 = 2
gr[3] = (a[4]-a[2])/2 = (11-6)/2 = 2.5
gr[4] = (a[5]-a[3])/2 = (14-7)/2 = 3.5
gr[5] = (a[5]-a[4])/1 = (14-11)/1 = 3
在前面的代码块中,我们计算了一维数组的梯度。 让我们添加另一个维度,并查看计算如何更改,如下所示:
[54]: a = np.array([1,3, 6, 7, 11, 14]). reshape(2,3)
gr = np.gradient(a)
gr
Out[54]: [array([[ 6., 8., 8.],
[ 6., 8., 8.]]), array([[ 2\. , 2.5, 3\. ],
[ 4\. , 3.5, 3\. ]])]
对于二维数组,与前面的代码一样,按列和按行计算梯度。 因此,结果将是两个数组的返回。 第一个数组代表行方向,第二个数组代表列方向。
总结
在本章中,我们介绍了线性代数的向量和矩阵运算。 我们研究了高级矩阵运算,尤其是特征点运算。 您还了解了的特征值和特征向量,然后在主成分分析(PCA)中实践了它们的用法。 此外,我们介绍了范数和行列式计算,并提到了它们在 ML 中的重要性和用法。 在最后两个小节中,您学习了如何将线性方程式转换为矩阵并求解它们,并研究了梯度的计算和重要性。
在下一章中,我们将使用 NumPy 统计数据进行解释性数据分析,以探索 2015 年美国住房数据。
三、使用 NumPy 统计函数对波士顿住房数据进行探索性数据分析
探索性数据分析(EDA)是数据科学项目的重要组成部分(如图数据科学过程所示)。 尽管在将任何统计模型或机器学习算法应用于数据之前这是非常重要的一步,但许多从业人员经常忽略或低估了它。
John Wilder Tukey 于 1977 年通过他的著作探索性数据分析促进了探索性数据分析。 在他的书中,他指导统计学家通过使用几种不同的视觉手段对统计数据集进行统计分析,这将帮助他们制定假设。 此外,在确定关键数据特征并了解有关数据的哪些问题后,EDA 还可以用于为高级建模准备分析。 在较高的层次上,EDA 是对您的数据的无假设探索,它利用了定量方法,使您可以可视化结果,从而可以识别模式,异常和数据特征。 在本章中,您将使用 NumPy 的内置统计方法执行探索性数据分析。
本章将涵盖以下主题:
- 加载和保存文件
- 探索数据集
- 查看基本统计量
- 计算平均值和方差
- 计算相关性
- 计算直方图
加载和保存文件
在本节中,您将学习如何加载/导入数据并保存。 加载数据的方式有很多,正确的方式取决于您的文件类型。 您可以加载/导入文本文件,SAS/Stata 文件,HDF5 文件以及许多其他文件。 HDF(分层数据格式)是一种流行的数据格式,用于存储和组织大量数据,并且在处理多维同构数组时非常有用。 例如,Pandas 库有一个非常方便的类,名为HDFStore,您可以在其中轻松使用 HDF5 文件。 在从事数据科学项目时,您很可能会看到许多这类文件,但是在本书中,我们将介绍最受欢迎的文件,例如 NumPy 二进制文件,文本文件(.txt)和逗号分隔值(.csv)文件。
如果内存和磁盘上有大量数据要管理,则可以使用bcolz库。 它提供了列式和压缩数据容器。 bcolz对象称为chunks,您在其中将整个数据压缩为位,然后在查询时部分解压缩。 压缩数据后,它会非常高效地使用存储。bcolz对象也提高了数据获取性能。 如果您对该库的性能感兴趣。 您可以在其官方 GitHub 存储库 上检查查询和速度比较。
使用数组时,通常在完成使用后将它们另存为 NumPy 二进制文件。 原因是您还需要存储数组形状和数据类型。 重新加载数组时,您希望 NumPy 记住它,并且您可以从上次中断的地方继续工作。 此外,即使您在具有不同架构的另一台计算机上打开文件, NumPy 二进制文件也可以存储有关数组的信息。 在 NumPy 中,load(),save(),savez()和savez_compressed()方法可帮助您加载和保存 NumPy 二进制文件,如下所示:
In [1]: import numpy as np
In [2]: example_array = np.arange(12).reshape(3,4)
In [3]: example_array
Out[3]: array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
In [4]: np.save('example.npy',example_array)
In [5]: d = np.load('example.npy')
In [6]: np.shape(d)
Out[6]: (3, 4)
In [7]: d
Out[7]: array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
在前面的代码中,我们执行以下步骤来练习将数组保存为二进制文件,以及如何在不影响其形状的情况下将其加载回:
- 创建形状为
(3, 4)的数组 - 将数组另存为二进制文件
- 加载回数组
- 检查形状是否仍然相同
同样,您可以使用savez()函数将多个数组保存到单个文件中。 如果要将文件另存为压缩的 NumPy 二进制文件,则可以按以下方式使用savez_compressed():
In [8]: x = np.arange(10)
y = np.arange(12)
np.savez('second_example.npz',x, y)
npzfile = np.load('second_example.npz')
npzfile.files
Out[8]: ['arr_0', 'arr_1']
In [9]: npzfile['arr_0']
Out[9]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
In [10]: npzfile['arr_1']
Out[10]: array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
In [11]: np.savez_compressed('compressed_example.npz', first_array = x , second_array = y)
npzfile = np.load('compressed_example.npz')
npzfile.files
Out[11]: ['first_array', 'second_array']
In [12]: npzfile['first_array']
Out[12]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
In [13]: npzfile['second_array']
Out[13]: array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
当您将多个数组保存在单个文件中时,如果您提供关键字参数如first_array=x,则将使用该名称保存数组。 否则,默认情况下,您的第一个数组将被赋予一个变量名,例如arr_0。 NumPy 具有称为loadtxt()的内置函数,用于从文本文件加载数据。 让我们加载一个.txt文件,该文件由一些整数和一个标头组成。
在前面的代码中,由于无法将字符串转换为浮点数,因此会出现误差,这实际上意味着您正在读取非数字值。 这样做的原因是该文件在顶部包含作为标题的字符串以及数值。 如果知道标题有多少行,则可以使用skiprows参数跳过这些行,如下所示:
In [15]: a = np.loadtxt("My_file.txt", delimiter='\t', skiprows=4)
a
Out[15]: array([ 0., 1., 2., 3., 4., 5., 6., 7., 8.,
9., 10., 11., 12., 13., 14., 15., 16., 17.,
18., 19., 20., 21., 22., 23., 24., 25., 26.,
27., 28., 29., 30., 31., 32., 33., 34., 35.,
36., 37., 38., 39., 40., 41., 42., 43., 44.,
45., 46., 47., 48., 49., 50., 51., 52., 53.,
54., 55., 56., 57., 58., 59., 60., 61., 62.,
63., 64., 65., 66., 67., 68., 69., 70., 71.,
72., 73., 74., 75., 76., 77., 78., 79., 80.,
81., 82., 83., 84., 85., 86., 87., 88., 89.,
90., 91., 92., 93., 94., 95., 96., 97., 98.,
99., 100., 101., 102., 103., 104., 105., 106., 107.,
108., 109., 110., 111., 112., 113., 114., 115., 116.,
117., 118., 119., 120., 121., 122., 123., 124., 125.,
126., 127., 128., 129., 130., 131., 132., 133., 134.,
135., 136., 137., 138., 139., 140., 141., 142., 143.,
144., 145., 146., 147., 148., 149., 150., 151., 152.,
153., 154., 155., 156., 157., 158., 159., 160., 161.,
162., 163., 164., 165., 166., 167., 168., 169., 170.,
171., 172., 173., 174., 175., 176., 177., 178., 179.,
180., 181., 182., 183., 184., 185., 186., 187., 188.,
189., 190., 191., 192., 193., 194., 195., 196., 197.,
198., 199., 200., 201., 202., 203., 204., 205., 206.,
207., 208., 209., 210., 211., 212., 213., 214., 215.,
216., 217., 218., 219., 220., 221., 222., 223., 224.,
225., 226., 227., 228., 229., 230., 231., 232., 233.,
234., 235., 236., 237., 238., 239., 240., 241., 242.,
243., 244., 245., 246., 247., 248., 249.])
另外,您可以使用genfromtxt()并将标头的转换默认设置为nan。 然后,您可以检测到标题占用了多少行,并使用skip_header参数跳过它们,如下所示:
In [16]: b = np.genfromtxt("My_file.txt", delimiter='\t')
b
Out[16]: array([ nan, nan, nan, nan, 0., 1., 2., 3., 4.,
5., 6., 7., 8., 9., 10., 11., 12., 13.,
14., 15., 16., 17., 18., 19., 20., 21., 22.,
23., 24., 25., 26., 27., 28., 29., 30., 31.,
32., 33., 34., 35., 36., 37., 38., 39., 40.,
41., 42., 43., 44., 45., 46., 47., 48., 49.,
50., 51., 52., 53., 54., 55., 56., 57., 58.,
59., 60., 61., 62., 63., 64., 65., 66., 67.,
68., 69., 70., 71., 72., 73., 74., 75., 76.,
77., 78., 79., 80., 81., 82., 83., 84., 85.,
86., 87., 88., 89., 90., 91., 92., 93., 94.,
95., 96., 97., 98., 99., 100., 101., 102., 103.,
104., 105., 106., 107., 108., 109., 110., 111., 112.,
113., 114., 115., 116., 117., 118., 119., 120., 121.,
122., 123., 124., 125., 126., 127., 128., 129., 130.,
131., 132., 133., 134., 135., 136., 137., 138., 139.,
140., 141., 142., 143., 144., 145., 146., 147., 148.,
149., 150., 151., 152., 153., 154., 155., 156., 157.,
158., 159., 160., 161., 162., 163., 164., 165., 166.,
167., 168., 169., 170., 171., 172., 173., 174., 175.,
176., 177., 178., 179., 180., 181., 182., 183., 184.,
185., 186., 187., 188., 189., 190., 191., 192., 193.,
194., 195., 196., 197., 198., 199., 200., 201., 202.,
203., 204., 205., 206., 207., 208., 209., 210., 211.,
212., 213., 214., 215., 216., 217., 218., 219., 220.,
221., 222., 223., 224., 225., 226., 227., 228., 229.,
230., 231., 232., 233., 234., 235., 236., 237., 238.,
239., 240., 241., 242., 243., 244., 245., 246., 247.,
248., 249.])
同样,您可以使用loadtxt(),genfromtxt()和savetxt()函数加载和保存.csv文件。 您唯一需要记住的是使用逗号作为定界符,如下所示:
In [17]: data_csv = np.loadtxt("MyData.csv", delimiter=',')
In [18]: data_csv[1:3]
Out[18]: array([[ 0.21982, 0.31271, 0.66934, 0.06072, 0.77785, 0.59984,
0.82998, 0.77428, 0.73216, 0.29968],
[ 0.78866, 0.61444, 0.0107 , 0.37351, 0.77391, 0.76958,
0.46845, 0.76387, 0.70592, 0.0851 ]])
In [19]: np.shape(data_csv)
Out[19]: (15, 10)
In [20]: np.savetxt('MyData1.csv',data_csv, delimiter = ',')
In [21]: data_csv1 = np.genfromtxt("MyData1.csv", delimiter = ',')
In [22]: data_csv1[1:3]
Out[22]: array([[ 0.21982, 0.31271, 0.66934, 0.06072, 0.77785, 0.59984,
0.82998, 0.77428, 0.73216, 0.29968],
[ 0.78866, 0.61444, 0.0107 , 0.37351, 0.77391, 0.76958,
0.46845, 0.76387, 0.70592, 0.0851 ]])
In [23]: np.shape(data_csv1)
Out[23]: (15, 10)
加载.txt文件时,它们会默认返回带有值的numpy数组,如后面的代码中所示:
In [24]: print (type(a))
print (type(b))
<class 'numpy.ndarray'>
<class 'numpy.ndarray'>
您可以使用tolist()方法将数据从数组更改为列表,然后使用savetxt()使用不同的分隔符将其保存为新文件,如下所示:
In [25]: c = a.tolist()
c
Out[25]: [0.0,
1.0,
2.0,
3.0,
4.0,
5.0,
6.0,
7.0,
8.0,
9.0,
10.0,
11.0,
12.0,
13.0,
14.0,
15.0,
16.0,
17.0,
18.0,
...
In [26]: np.savetxt('My_List.txt',c, delimiter=';')
In [27]: myList = np.loadtxt("My_List.txt", delimiter=';')
type(myList)
Out[27]: numpy.ndarray
将列表保存到My_List.txt后,可以使用loadtxt()加载此文件,它将再次作为numpy数组返回。 如果要返回数组的字符串表示形式,可以使用array_str(),array_repr()或array2string()方法,如下所示:
In [28]: d = np.array_str(a,precision=1)
d
Out[28]: '[ 0\. 1\. 2\. 3\. 4\. 5\. 6\. 7\. 8\. 9\. 10\. 11.\n 12\. 13\. 14\. 15\. 16\. 17\. 18\. 19\. 20\. 21\. 22\. 23.
24\. 25\. 26\. ... ]'
即使array_str()和array_repr()看起来一样,array_str()返回数组内部数据的字符串表示形式,而array_repr()实际上返回数组的字符串表示形式。 因此,array_repr()返回有关数组类型及其数据类型的信息。 这两个函数在内部都使用array2string(),这实际上是字符串格式化函数最灵活的版本,因为它具有更多可选参数。 以下代码块使用load_boston()方法加载波士顿房屋数据集:
In [29]: from sklearn.datasets import load_boston
dataset = load_boston()
dataset
在本章中,您将对sklearn.datasets包中的示例数据集进行探索性数据分析。 该数据集是关于波士顿房价的。 在前面的代码中,load_boston()函数是从sklearn.datasets包中导入的,如您所见,它返回具有属性DESCR,data,feature_names和target的类似字典的对象 ]。 这些属性的详细信息如下:
| 属性 | 解释 |
|---|---|
DESCR |
数据集的完整描述 |
data |
特征列 |
feature_names |
特征名称 |
target |
标签数据 |
在本节中,您学习了如何使用numpy函数加载和保存文件。 在下一部分中,您将探索波士顿住房数据集。
探索我们的数据集
在本节中,您将探索数据集并对其进行质量检查。 您将检查数据形状是什么,以及它的数据类型,所有缺失值/ NaN,拥有多少个特征列以及每个列代表什么。 让我们开始加载数据并进行探索:
In [30]: from sklearn.datasets import load_boston
dataset = load_boston()
samples,label, feature_names = dataset.data , dataset.target , dataset.feature_names
In [31]: samples.shape
Out[31]: (506, 13)
In [32]: label.shape
Out[32]: (506,)
In [33]: feature_names
Out[33]: array(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT'],
dtype='<U7')
在前面的代码中,您加载了数据集并解析了数据集的属性。 这表明我们拥有具有13函数的506样本,并且具有506标签(回归目标)。 如果要阅读数据集的描述,可以使用print(dataset.DESCR)。 由于此代码的输出太长,无法放置在此处。
如第一章所示,您可以使用dtype检查数组的数据类型。 如下面的代码所示,示例的每一列中都有一个数字float64数据类型和一个标签。 检查数据类型是非常重要的一步,您可能会意识到类型和列描述之间存在一些不一致,或者,如果您认为使用不太精确的目标值仍然可以实现,则可以通过更改其数据类型来减少数组的内存大小:
In [35]: print(samples.dtype)
print(label.dtype)
float64
float64
缺失值处理在 Python 软件包中略有不同。numpy库没有缺失值。 如果您的数据集中缺少值,则导入后它们将转换为NaN。 NumPy 中非常常见的方法是使用掩码数组以忽略NaN值,这在第一章中已向您展示:
In [36]: np.isnan(samples)
Out[36]: array([[False, False, False, ..., False, False, False],
[False, False, False, ..., False, False, False],
[False, False, False, ..., False, False, False],
...,
[False, False, False, ..., False, False, False],
[False, False, False, ..., False, False, False],
[False, False, False, ..., False, False, False]], dtype=bool)
In [37]: np.isnan(np.sum(samples))
Out[37]: False
In [38]: np.isnan(np.sum(label))
Out[38]: False
要针对数据中的NaN值逐元素进行测试,可以使用isnan()方法。 此方法将返回一个布尔数组。 对于大型数组而言,检测它是否返回true可能很麻烦。 在这种情况下,您可以将数组的np.sum()用作isnan()的参数,这样它将为结果返回单个布尔值。
在本节中,您将深入研究数据并进行常规质量检查。 在下一节中,我们将继续进行基本统计。
查看基本统计量
在本节中,您将从统计分析的第一步开始,计算数据集的基本统计信息。 即使 NumPy 的内置统计函数有限,我们也可以将其与 SciPy 结合使用。 在开始之前,让我们描述一下我们的分析将如何进行。 所有特征列和标签列都是数字,但您可能已经注意到 Charles River 虚拟变量(CHAS)列具有二进制值(0, 1),这意味着它实际上是根据分类数据编码的。 分析数据集时,可以将列分为Categorical和Numerical。 为了一起分析它们,应将一种类型转换为另一种类型。 如果您具有分类值,并且想要将其转换为数字值,则可以通过将每个类别转换为数字值来实现。 该过程称为编码。 另一方面,可以通过将数值转换为类别对应物来执行装箱,类别对应物是通过将数据分成间隔来创建的。
我们将通过逐一探讨其特征来开始分析。 在统计中,此方法称为单变量分析。 单变量分析的目的主要围绕描述。 我们将计算最小值,最大值,范围,百分位数,均值和方差,然后绘制一些直方图并分析每个特征的分布。 我们将介绍偏度和峰度的概念,然后看一下修剪的重要性。 完成单变量分析后,我们将继续进行双变量分析,这意味着同时分析两个特征。 为此,我们将探索两组特征之间的关系:
In [39]: np.set_printoptions(suppress=True, linewidth=125)
minimums = np.round(np.amin(samples, axis=0), decimals=1)
maximums = np.round(np.amax(samples, axis=0), decimals=1)
range_column = np.round(np.ptp(samples, axis=0), decimals=1)
mean = np.round(np.mean(samples, axis=0), decimals=1)
median = np.round(np.median(samples, axis=0), decimals=1)
variance = np.round(np.var(samples, axis=0), decimals=1)
tenth_percentile = np.round(np.percentile(samples, 10, axis=0), decimals = 1)
ninety_percentile = np.round(np.percentile(samples, 90 ,axis=0), decimals = 1)
In [40]: range_column
Out[40]: array([ 89\. , 100\. , 27.3, 1\. , 0.5, 5.2, 97.1, 11\. , 23\. , 524\. , 9.4, 396.6, 36.2])

在前面的代码中,我们首先使用set_printoptions()方法设置打印选项,以便查看四舍五入的小数位数,并且其线宽足以容纳所有列。 要计算基本统计信息,我们使用numpy函数,例如amin(),amax(),mean(),median(),var(),percentile()和ptp()。 所有计算都是按列进行的,因为每一列都代表一个要素。 最终的数组看起来有点草率且无用,因为您看不到哪行显示了哪些统计信息:
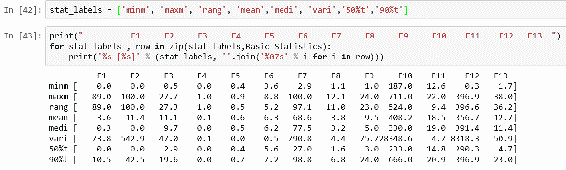
为了打印对齐的 numpy 数组,可以使用zip()函数添加行标签并在数组之前打印列标签。 在 SciPy 中,您可以使用更多统计函数来计算基本统计信息。 SciPy 提供describe()函数,该函数返回给定数组的一些描述性统计信息。 您可以使用一个函数来计算点,最小值,最大值,均值,方差,偏度和峰度,然后分别解析它们,如下所示:

以下代码块分别计算基本统计信息并将其堆叠到最终数组中:
In [45]: minimum = arr.minmax[0]
maximum = arr.minmax[1]
mean = arr.mean
median = np.round(np.median(samples,axis = 0), decimals = 1)
variance = arr.variance
tenth_percentile = stats.scoreatpercentile(samples, per = 10, axis = 0)
ninety_percentile = stats.scoreatpercentile(samples, per =90, axis = 0)
rng = stats.iqr(samples, rng = (20,80), axis = 0)
np.set_printoptions(suppress = True, linewidth = 125)
Basic_Statistics1 = np.round(np.vstack((minimum,maximum,rng, mean,median,variance,tenth_percentile,ninety_percentile)), Basic_Statistics1.shape
Out[45]: (8, 13)
In [46]: stat_labels1 = ['minm', 'maxm', 'rang', 'mean', 'medi', 'vari', '50%t', '90%t']
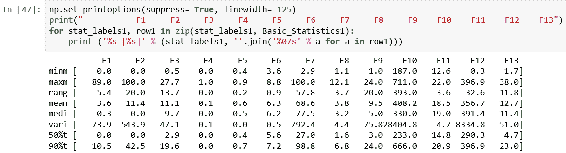
与 NumPy 相比,我们可以使用iqr()函数来计算范围。 此函数计算沿指定轴和范围(rng参数)的数据的四分位数范围。 默认情况下,rng = (25, 75),这意味着该函数将计算数据的第 75 和第 25 个百分位数之间的差。 为了返回与numpy.ptp()函数相同的输出,可以使用rng = (0, 100),因为这将计算所有给定数据的范围。 我们使用stat.scoreatpercentile()作为与numpy.percentile()方法的等效物,来计算特征的第 10 个和第 90 个百分位值。 如果您看一眼结果,您会发现几乎每个特征的差异都很大。 您可以看到,由于我们通过将参数传递为(20,80)来限制范围计算,因此范围值显着减小。 它也向您展示了我们在分布式要素的两侧都有许多极值。 从我们的结果可以得出结论,对于大多数特征,平均值均高于中位数,这表明我们这些特征的分布偏向右侧。 在下一节中,当我们绘制直方图然后深入分析这些特征的偏度和峰度时,您将清楚地看到这一点。
计算直方图
直方图是数字数据分布的直观表示。 一百多年前,卡尔·皮尔森(Karl Pearson)首次提出了这一概念。 直方图是一种用于连续数据的条形图,而条形图直观地表示类别变量。 第一步,您需要将整个值范围划分为一系列间隔(仓位)。 每个桶必须相邻,并且它们不能重叠。 通常,桶大小相等,要包含的桶数量的经验法则是 5–20。 这意味着,如果您有 20 个以上的容器,则图形将很难阅读。 相反,如果您的箱数少于 5 个,则您的图形将很少了解数据的分布:
In [48]: %matplotlib notebook
%matplotlib notebook
import matplotlib.pyplot as plt
NOX = samples[:,5:6]
plt.hist(NOX,bins ='auto')
plt.title("Distribution nitric oxides concentration (parts per 10 million)")
plt.show()
在前面的代码中,我们绘制了特征NOX的直方图。 箱柜计算自动完成,如下所示:
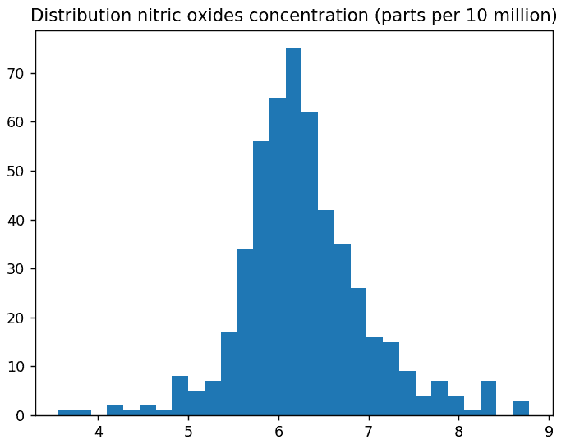
您可以通过将切片数组作为第一个参数,使用pyplot.hist()绘制直方图。 y 轴显示数据集中每个间隔(桶)中有多少值的计数, x 轴表示其值。 通过设置normed=True,您可以看到箱柜的百分比,如下所示:
In [49]: plt.hist(NOX,bins ='auto', normed = True)
plt.title("Distribution nitric oxides concentration (parts per 10 million)")
plt.show()
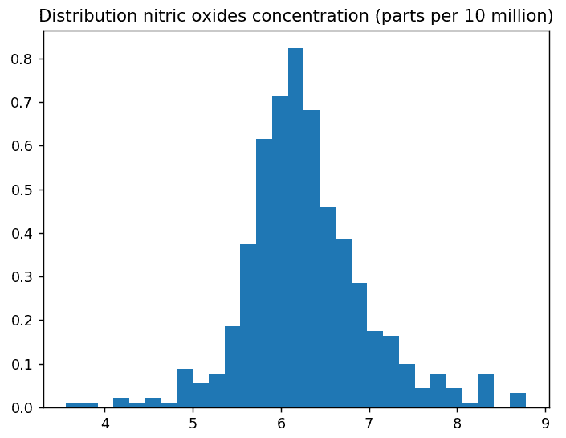
当您查看直方图时,可能很难计算每个桶及其边界的大小。 当pyplot.hist()返回包含此信息的元组时,您可以轻松地获得这些值,如下所示:
In [50]: import matplotlib.pyplot as plt
NOX = samples[:,5:6]
n, bins, patches = plt.hist(NOX, bins='auto')
print('Bin Sizes')
print(n)
print('Bin Edges')
print(bins)
在前面的代码中,我们打印出每个桶中包含多少个数字,以及桶的边界是什么,如下所示:

让我们解释一下前面的输出。 第一个桶的大小为1,这意味着此桶中仅存在一个值下降。 第一仓的间隔在3.561和3.74096552之间。 为了使它们更整洁,可以使用以下代码块,该代码块有意义地堆叠了这两个数组(bin_interval,bin_size):
In [51]: bins_string = bins.astype(np.str)
n_string = n.astype(np.str)
lists = []
for i in range(0, len(bins_string)-1):
c = bins_string[i]+ "-" + bins_string[i+1]
lists.append(c)
new_bins = np.asarray(lists)
Stacked_Bins = np.vstack((new_bins, n_string)).T
Stacked_Bins

确定桶的数量及其宽度非常重要。 一些理论家对此进行试验以确定最佳拟合。 下表显示了最受欢迎的估计器。 您可以将估计器设置为numpy.histogram()中的bins参数,以相应地更改桶计算。 这些方法由pyplot.hist()函数隐式支持,因为其参数传递给numpy.histogram():
| 估计器 | 公式 |
|---|---|
| Freedman-Diaconis 估计 | 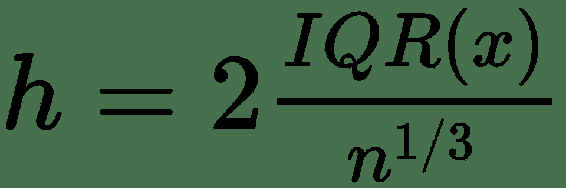 |
| Doane 公式 | 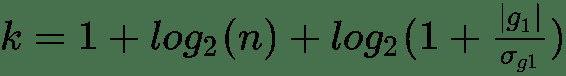 |
| Rice 法则 | 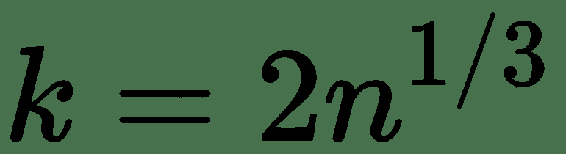 |
| Scott 的常规参考法则 | 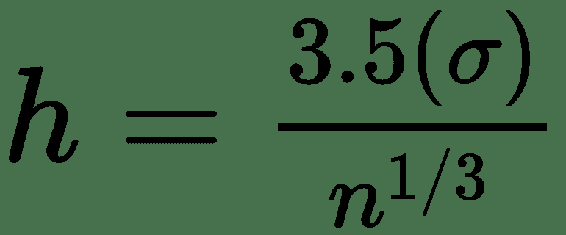 |
| Sturges 公式 | 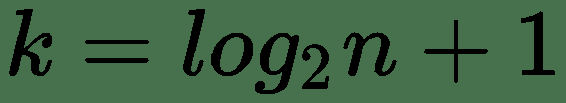 |
| 平方根选项 | 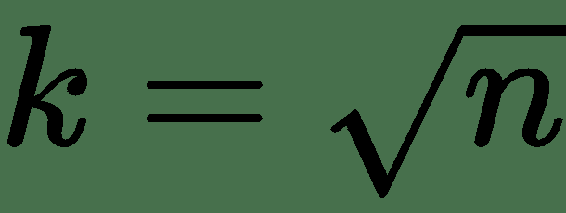 |
IQR =四分位间距
g[1] =分布的估计三阶偏度
所有这些方法都有不同的优势。 例如,Strurges 公式对于高斯数据是最佳的。 Rice 的规则是 Sturges 公式的简化版本,并假定近似正态分布,因此,如果数据不是正态分布,则可能效果不佳。 Doane 的公式是 Sturges 公式的改进版本,尤其是在具有非正态分布的情况下。 Freedman–Diaconis 估计器是 Scott 规则的修改版本,他用IQR=2代替了 3.5 个标准差,这使公式对异常值的敏感性降低。 平方根选择是一种非常常见的方法,许多工具都以其快速简便的方式使用它。 在numpy.histogram()中,还有一个名为'auto'的选项,它为我们提供了最大的 Sturges 和 Freedman–Diaconis 估计器方法。 让我们看看这些方法将如何影响直方图:
In [52]: fig, ((ax1, ax2, ax3),(ax4,ax5,ax6)) = plt.subplots(2,3,sharex=True)
axs = [ax1,ax2,ax3,ax4,ax5,ax6]
list_methods = ['fd','doane', 'scott', 'rice', 'sturges','sqrt']
plt.tight_layout(pad=1.1, w_pad=0.8, h_pad=1.0)
for n in range(0, len(axs)):
axs[n].hist(NOX,bins = list_methods[n])
axs[n].set_title('{}'.format(list_methods[n]))
在前面的代码中,我们编译了六个直方图,它们全部共享相同的 x 轴,如下所示:
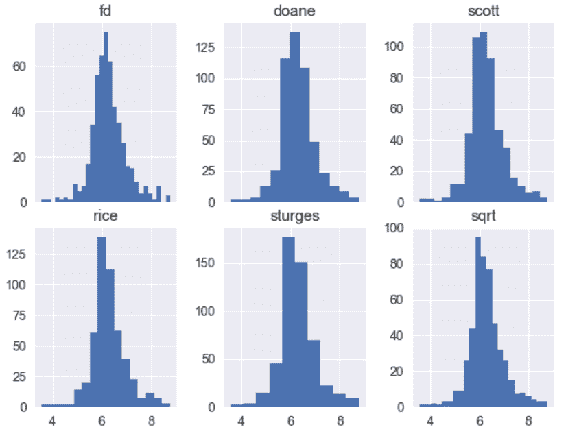
所有直方图都表示相同的特征,但具有不同的合并方法。 例如,fd方法显示数据看起来接近其正态分布,而另一方面,doane方法看起来更像学生的 T 分布。 另外,sturges方法会创建两个小容器,因此很难分析数据。 当我们查看基本统计数据时,我们指出大多数特征的均值均高于其中位数,因此他们将数据向右倾斜。 但是,如果您查看sturges,rice和sqrt方法,则很难这么说。 但是,当我们使用自动箱绘制直方图时,这是显而易见的:
In [53]: import numpy as np
samples_new = np.delete(samples, 3 , axis=1)
samples_new.shape
Out[53]: (506, 12)
In [54]: %matplotlib notebook
%matplotlib notebook
import matplotlib.pyplot as plt
fig,((ax1, ax2 , ax3),(ax4, ax5, ax6), (ax7, ax8, ax9), (ax10, ax11, ax12)) = plt.subplots(4,3, figsize = (10,15))
axs =[ax1, ax2 , ax3, ax4, ax5, ax6, ax7, ax8, ax9, ax10, ax11, ax12]
feature_names_new = np.delete(feature_names,3)
for n in range(0, len(axs)):
axs[n].hist(samples_new[:,n:n+1], bins ='auto', normed = True)
axs[n].set_title('{}'.format(feature_names[n]))
在前面的代码中,我们在单个布局中编译所有特征直方图。 这将帮助我们轻松比较它们。 前面代码的输出如下:
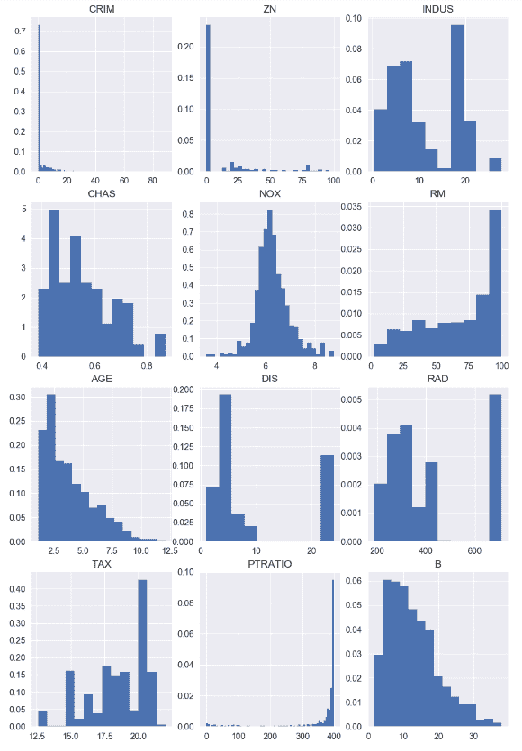
在前面的代码中,我们删除了CHAS,因为它包含二进制值,这意味着直方图将无助于我们进一步了解此特征。 我们还从特征列表中取出了特征名称,以便正确绘制其余特征。
从这些图表我们可以得出结论,在大多数城镇中,人均犯罪率非常低,但是在某些城镇中,这一比例非常高。 通常,住宅用地面积低于 25,000 英尺。在许多情况下,非零售业务用地所占土地不到整个城镇的 10% 。 另一方面,我们可以看到许多城镇的非零售业务用地约为 20% 。 一氧化氮的浓度非常偏斜,尽管此处存在一些离平均值很远的异常值。 每个住宅的平均房间数在 5 至 7 间之间。 在 1940 年之前建造的架构物中,超过 50% 的架构物被其所有者占用。 他们中的大多数人离波士顿的就业中心都不远。 超过 10% 的人无法轻松到达径向公路。 对于相当多的人来说,财产税很高。 通常,教室规模为 15 至 20 个孩子。 大多数城镇中居住的黑人比例非常相似。 大多数城镇居民的经济地位较低。 通过查看这些直方图,您可以得出许多其他结论。 如您所见,直方图在描述数据的分布方式时非常有用,并且可以看到平均值,方差和离群值。 在下一节中,我们将重点介绍偏度和峰度。
解释偏度和峰度
在统计分析中,力矩是一种定量度量,用于描述距参考点的预期距离。 如果期望参考点,则将其称为中心矩。 在统计中,中心矩是与均值相关的矩。 第一个和第二个矩分别是平均值和方差。 平均值是您的数据点的平均值。 方差是每个数据点与平均值的总偏差。 换句话说,方差表明您的数据如何与均值分散。 第三个中心矩是偏度,它测量均值分布的不对称性。 在标准正态分布中,偏度是对称的,因此等于零。 另一方面,如果均值
In [55]: %matplotlib notebook
%matplotlib notebook
from scipy.stats import skewnorm
fig, (ax1, ax2, ax3) = plt.subplots(1,3 ,figsize=(10,2.5))
x1 = np.linspace(skewnorm.ppf(0.01,-3), skewnorm.ppf(0.99,-3),100)
x2 = np.linspace(skewnorm.ppf(0.01,0), skewnorm.ppf(0.99,0),100)
x3 = np.linspace(skewnorm.ppf(0.01,3), skewnorm.ppf(0.99,3),100)
ax1.plot(skewnorm(-3).pdf(x1),'k-', lw=4)
ax2.plot(skewnorm(0).pdf(x2),'k-', lw=4)
ax3.plot(skewnorm(3).pdf(x3),'k-', lw=4)
ax1.set_title('Left Skew')
ax2.set_title('Normal Dist')
ax3.set_title('Right Skew')
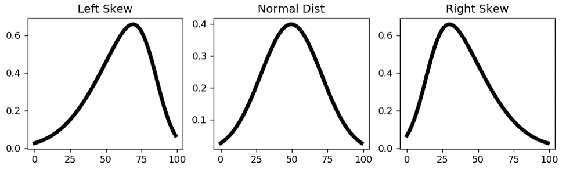
您可以使用skewnorm()函数轻松创建具有偏斜度的正态分布。 如您在前面的代码中看到的,我们生成一个具有 100 个值的百分点函数(与累积分布函数百分位数相反),然后创建具有不同偏斜度的线。 您不能直接得出结论,左偏斜比右偏斜好,反之亦然。 当分析数据的偏斜度时,您需要考虑这些尾巴会导致什么。 例如,如果您正在分析股票收益的时间序列,并将其绘制后看到一个正确的偏斜,则不必担心获得比预期更高的收益,因为这些离群值不会给您的股票带来任何风险。 交易策略。 当您分析服务器的响应时间时,可能会出现类似的示例。 当您绘制响应时间的概率密度函数时,您对左尾巴并不真正感兴趣,因为它们代表了快速的响应时间。
关于均值的第四个中心矩是峰度。 峰度描述了与分布曲线的平坦程度或变薄程度有关的尾部(离群值)。 在正态分布中,峰度等于 3。峰度主要有三种类型:Leptokurtic(薄),Mesokurtic和Platykurtic(平坦):
In [56]: %matplotlib notebook
%matplotlib notebook
import scipy
from scipy import stats
import matplotlib.pyplot as plt
fig, (ax1, ax2, ax3) = plt.subplots(1, 3 , figsize=(10,2))
axs= [ax1, ax2, ax3]
Titles = ['Mesokurtic', 'Lebtokurtic', 'Platykurtic']
#Mesokurtic Distribution - Normal Distribution
dist = scipy.stats.norm(loc=100, scale=5)
sample_norm = dist.rvs(size = 10000)
#leptokurtic Distribution
dist2 = scipy.stats.laplace(loc= 100, scale= 5)
sample_laplace = dist2.rvs(size= 10000)
#platykurtic Distribution
dist3 = scipy.stats.cosine(loc= 100, scale= 5)
sample_cosine = dist3.rvs(size= 10000)
samples = [sample_norm, sample_laplace, sample_cosine]
for n in range(0, len(axs)):
axs[n].hist(samples[n],bins= 'auto', normed= True)
axs[n].set_title('{}'.format(Titles[n]))
print ("kurtosis of" + Titles[n])
print(scipy .stats.describe(samples[n])[5])
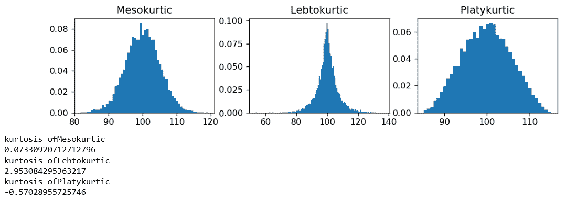
在前面的代码中,您可以更清楚地看到分布形状的差异。 所有峰度值均使用stats.describe()方法进行归一化,因此正态分布的实际峰度值约为 3,而归一化版本为 0.02。 让我们快速检查一下我们特征的偏度和峰度值是什么:
In [57]: samples,label, feature_names = dataset.data , dataset.target , dataset.feature_names
for n in range(0, len(feature_names_new)):
kurt = scipy.stats.describe(samples[n])[5]
skew = scipy.stats.describe(samples[n])[4]
print (feature_names_new[n] + "-Kurtosis: {} Skewness: {}" .format(kurt, skew))
CRIM-Kurtosis: 2.102090573040533 Skewness: 1.9534138515494224
ZN-Kurtosis: 2.8706349006925134 Skewness: 2.0753333576721893
INDUS-Kurtosis: 2.9386308786131767 Skewness: 2.1061627843164086
NOX-Kurtosis: 3.47131446484547 Skewness: 2.2172838215060517
RM-Kurtosis: 3.461596258869246 Skewness: 2.2086627738768234
AGE-Kurtosis: 3.395079726813977 Skewness: 2.1917520072643533
DIS-Kurtosis: 1.9313625761956317 Skewness: 1.924572804475305
RAD-Kurtosis: 1.7633603556547106 Skewness: 1.8601991629604233
TAX-Kurtosis: 1.637076772210217 Skewness: 1.8266096199819994
PTRATIO-Kurtosis: 1.7459544645159752 Skewness: 1.8679592455694167
B-Kurtosis: 1.7375702020429316 Skewness: 1.8566444885400044
LSTAT-Kurtosis: 1.8522036606250456 Skewness: 1.892802610207445
从结果中可以看出,所有特征都具有正偏度,这表明它们向右偏斜。 就峰度而言,它们都具有正值,尤其是 NOX 和 RM,它们具有非常高的色氨酸。 我们可以得出结论,它们全都是瘦腿型的,这表明数据更加集中在均值上。 在下一节中,我们将着重于数据修整并使用修整后的数据计算统计数据。
整理统计量
正如您在上一节中已经注意到的那样,我们特征的分布非常分散。 处理模型中的异常值是分析中非常重要的部分。 当您查看描述性统计数据时,它也非常重要。 由于这些极端值,您很容易混淆并曲解分布。 SciPy 具有非常广泛的统计函数,可以计算有关修剪数据的描述性统计数据。 使用调整后的统计数据的主要思想是删除异常值(尾部),以减少其对统计计算的影响。 让我们看看如何使用这些函数,以及它们如何影响我们的特征分布:
In [58]: np.set_printoptions(suppress= True, linewidth= 125)
samples = dataset.data
CRIM = samples[:,0:1]
minimum = np.round(np.amin(CRIM), decimals=1)
maximum = np.round(np.amax(CRIM), decimals=1)
variance = np.round(np.var(CRIM), decimals=1)
mean = np.round(np.mean(CRIM), decimals=1)
Before_Trim = np.vstack((minimum, maximum, variance, mean))
minimum_trim = stats.tmin(CRIM, 1)
maximum_trim = stats.tmax(CRIM, 40)
variance_trim = stats.tvar(CRIM, (1,40))
mean_trim = stats.tmean(CRIM, (1,40))
After_Trim = np.round(np.vstack((minimum_trim,maximum_trim,variance_trim,mean_trim)), decimals=1)
stat_labels1 = ['minm', 'maxm', 'vari', 'mean']
Basic_Statistics1 = np.hstack((Before_Trim, After_Trim))
print (" Before After")
for stat_labels1, row1 in zip(stat_labels1, Basic_Statistics1):
print ('%s [%s]' % (stat_labels1, ''.join('%07s' % a for a in row1)))
Before After
minm [ 0.0 1.0]
maxm [ 89.0 38.4]
vari [ 73.8 48.1]
mean [ 3.6 8.3]
要计算调整后的统计信息,我们使用了tmin(),tmax(),tvar()和tmean(),如前面的代码所示。 所有这些函数都将极限值作为第二个参数。 在CRIM函数中,我们可以在右侧看到很多尾巴,因此我们将数据限制为(1, 40),然后计算统计信息。 在修整值之前和之后,您可以通过比较计算的统计信息来观察差异。 作为tmean()的替代方法,如果要从两侧按比例分割数据,可以使用trim_mean()函数。 您可以看到我们的均值和方差在修剪数据后如何显着变化。 当我们删除了 40 至 89 之间的许多极端离群值时,方差显着减小。相同的修整对均值有不同的影响,此后均值增加了一倍以上。 原因是先前的分布中有很多零,并且通过将计算限制在 1 和 40 的值之间,我们删除了所有这些零,这导致了更高的平均值。 请注意,上述所有函数只是在计算这些值时即时修剪数据,因此CRIM数组不会被修剪。 如果要从两侧修剪数据,则可以在一侧使用trimboth()和trim1()。 在这两种方法中,应该使用比例作为参数,而不是使用极限值。 例如,如果您传递proportiontocut =0.2,它将把您最左边和最右边的值切成 20% :
In [59]: %matplotlib notebook
%matplotlib notebook
import matplotlib.pyplot as plt
CRIM_TRIMMED = stats.trimboth(CRIM, 0.2)
fig, (ax1, ax2) = plt.subplots(1,2 , figsize =(10,2))
axs = [ax1, ax2]
df = [CRIM, CRIM_TRIMMED]
list_methods = ['Before Trim', 'After Trim']
for n in range(0, len(axs)):
axs[n].hist(df[n], bins = 'auto')
axs[n].set_title('{}'.format(list_methods[n]))
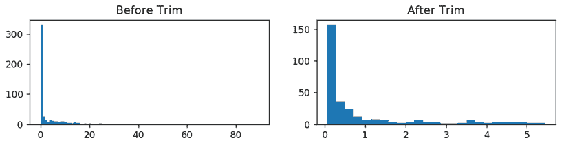
从两侧修剪掉 20% 的值后,我们可以更好地解释分布,实际上可以看到大多数值在 0 到 1.5 之间。 仅查看左方的直方图就很难获得这种见解,因为极值主导了直方图,并且我们只能看到 0 周围的一条线。因此,trimmed函数在探索性数据分析中非常有用。 在下一部分中,我们将重点讨论箱形图,它们对于数据的描述性分析和异常值检测非常有用且非常流行。
箱形图
探索性数据分析中的另一个重要视觉效果是箱形图,也称为箱须图。 它基于五位数摘要建立,该摘要是最小值,第一四分位数,中位数,第三四分位数和最大值。 在标准箱形图中,这些值表示如下:
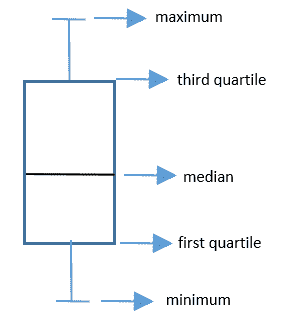
这是比较几种分布的一种非常方便的方法。 通常,情节的胡须通常延伸到极限点。 或者,您可以将其切入 1.5 个四分位范围。 让我们检查一下CRIM和RM函数:
In [60]: %matplotlib notebook
%matplotlib notebook
import matplotlib.pyplot as plt
from scipy import stats
samples = dataset.data
fig, (ax1,ax2) = plt.subplots(1,2, figsize =(8,3))
axs = [ax1, ax2]
list_features = ['CRIM', 'RM']
ax1.boxplot(stats.trimboth(samples[:,0:1],0.2))
ax1.set_title('{}'.format(list_features[0]))
ax2.boxplot(stats.trimboth(samples[:,5:6],0.2))
ax2.set_title('{}'.format(list_features[1]))
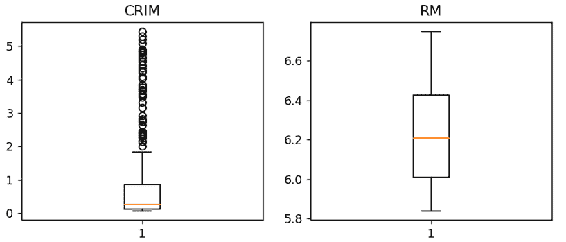
正如您在前面的代码中看到的那样,RM 值一直沿最小值和最大值连续分散,以便胡须看起来像一条线。 您可以轻松地检测到中位数几乎位于第一和第三四分位数之间的中间位置。 在CRIM中,极值不会沿着最小值继续; 它们更像是单个外围数据点,因此表示就像一个圆圈。 您可以看到这些离群值大多位于第三个四分位数之后,并且中位数非常接近第一个四分位数。 由此,您还可以得出结论,分布是右偏的。 因此,箱形图是直方图的非常有用的替代方法,因为您可以轻松分析分布并一次比较多个分布。 在下一节中,我们将继续进行双变量分析,并研究标签数据与要素的相关性。
计算相关性
本节专门用于双变量分析,您可以在其中分析两列。 在这种情况下,我们通常研究这两个变量之间的关联,这称为相关性。 相关性显示两个变量之间的关系,并回答一些问题,例如,如果变量 B 增加 10% ,变量 A 将会发生什么? 在本节中,我们将说明如何计算数据的相关性并以二维散点图表示它。
通常,相关是指任何统计依赖性。 相关系数是计算相关度量的定量值。 您可以将相关性和相关系数之间的关系视为湿度计和湿度之间的相似关系。 相关系数最流行的类型之一是皮尔逊积矩相关系数。 相关系数的值在 +1 和 -1 之间,其中 -1 表示两个变量之间的强负线性关系,而 +1 表示两个变量之间的强正线性关系。 在 NumPy 中,我们可以使用corrcoef()方法来计算系数相关矩阵,如下所示:
In [61]: np.set_printoptions(suppress= True, linewidth = 125)
CorrelationCoef_Matrix = np.round(np.corrcoef(samples, rowvar= False), decimals= 1)
CorrelationCoef_Matrix

Seaborn 是一个基于 matplotlib 的统计数据可视化库,您可以使用它创建非常吸引人的美观统计图形。 它是一个非常受欢迎的库,具有精美的可视化效果,并且与流行的软件包(尤其是 Pandas)具有完美的兼容性。 您可以使用seaborn程序包中的热图来形象化相关系数矩阵。 当您具有数百种特征时,它对于检测高相关系数非常有用:
In [62]: CorrelationCoef_Matrix1 = np.round(np.corrcoef(samples, rowvar= False), decimals= 1)
CorrelationCoef_Matrix1
import seaborn as sns; sns.set()
ax = sns.heatmap(CorrelationCoef_Matrix1, cmap= "YlGnBu")
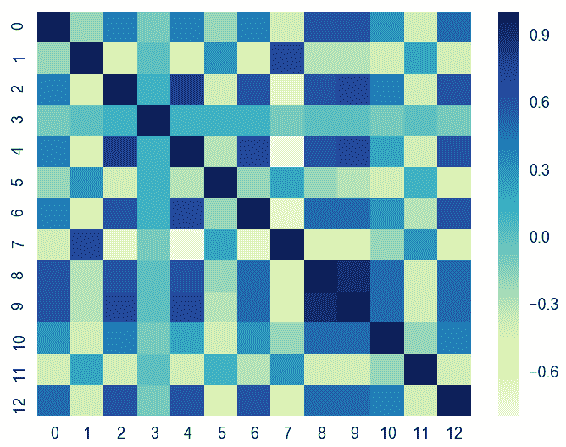
在这里,我们具有标签列特征的相关系数。 您可以在corrcoef()函数中添加其他变量集作为第二个参数,就像我们对label列所做的那样,如下面的屏幕快照所示。 只要形状相同,该函数将在最后堆叠此列并计算相关系数矩阵:

如您所见,除了F13之外,大多数特征都具有弱或中等的负线性关系。 另一方面,F6具有很强的正线性关系。 让我们绘制此特征并用散点图查看这种关系。 以下代码块借助matplotlib显示了三个不同的特征散点图(RM,DIS和LSTAT)和一个标签列:
In [64]: %matplotlib notebook
%matplotlib notebook
import matplotlib.pyplot as plt
from scipy import stats
fig, (ax1, ax2, ax3) = plt.subplots(1,3 ,figsize= (10,4))
axs =[ax1,ax2,ax3]
feature_list = [samples[:,5:6], samples[:,7:8], samples[:,12:13]]
feature_names = ["RM", "DIS", "LSTAT"]
for n in range(0, len(feature_list)):
axs[n].scatter(label, feature_list[n], edgecolors=(0, 0, 0))
axs[n].set_ylabel(feature_names[n])
axs[n].set_xlabel('label')
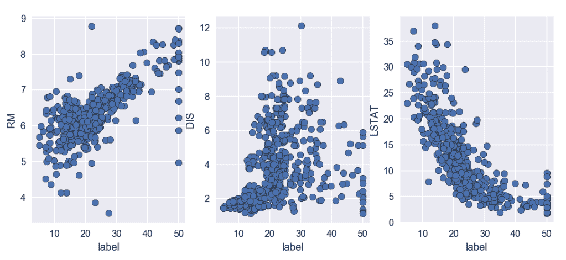
在前面的代码中,RM 和标签值分散为一条正线性线,这与相关系数值为 0.7 一致,如前面的屏幕快照所示。 散点图表明样品的 RM 值越高,标签的值越高。 在中间的散点图中,您可以看到系数相关性等于 0.25 的位置。 这显示出非常弱的正线性相关性,这在散点图中也可以看到。 我们可以得出结论,由于值分散在各处,因此没有明确的关系。 第三个散点图显示了强大的线性关系,相关系数为 -0.7。 随着LSTAT下降,标签值开始增加。 所有这些相关矩阵和散点图均使用未修剪的数据对此进行了计算。 让我们看看如何针对每个要素和标签从两侧修剪数据 10% 来改变数据集的线性关系结果:
In [65]: %matplotlib notebook
%matplotlib notebook
import matplotlib.pyplot as plt
from scipy import stats
fig, (ax1, ax2, ax3) = plt.subplots(1,3 ,figsize= (9,4))
axs = [ax1, ax2, ax3]
RM_tr = stats.trimboth(samples[:,5:6],0.1)
label_tr = stats.trimboth(label, 0.1)
LSTAT_tr = stats.trimboth(samples[:,12:13],0.1)
DIS_tr = stats.trimboth(samples[:,7:8],0.1)
feature_names = ["RM", "DIS", "LSTAT"]
feature_list = [RM_tr, DIS_tr, LSTAT_tr]
for n in range(0, len(feature_list)):
axs[n].scatter(label_tr,feature_list[n], edgecolors=(0, 0, 0))
axs[n].set_ylabel(feature_names[n])
axs[n].set_xlabel('label')
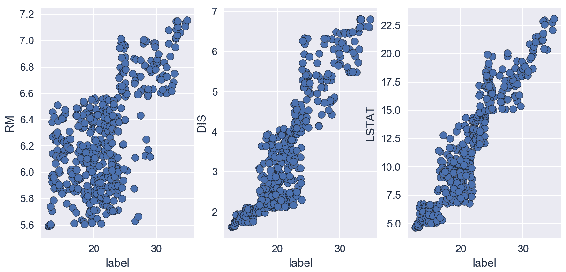
修剪数据后,您可以看到所有特征都与标签具有很强的正线性相关性,尤其是DIS和LSTAT的相关性,其中标签发生了巨大变化。 这显示了修剪的力量。 如果您不知道如何处理异常值,则很容易误解您的数据。 离群值可以更改分布的形状以及其他变量之间的相关性,最终它们可以影响模型的性能。
总结
在本章中,我们介绍了使用 NumPy,SciPy,matplotlib 和 Seaborn 软件包进行探索性数据分析的过程。 首先,我们学习了如何加载和保存文件以及探索数据集。 然后,我们解释并计算了重要的统计中心矩,例如均值,方差,偏度和峰度。 四个重要的可视化分别用于单变量和变量分析的图形表示; 这些是直方图,箱形图,散点图和热图。 还通过示例强调了数据修整的重要性。
在下一章中,我们将更进一步,并开始使用线性回归预测房价。
四、使用线性回归预测房价
在本章中,我们将通过实现线性回归来介绍监督学习和预测建模。 在上一章中,您了解了探索性分析的知识,但尚未研究建模。 在本章中,我们将创建一个线性回归模型来预测房地产市场价格。 广义上讲,我们将借助目标变量与其他变量的关系来预测目标变量。 线性回归被广泛使用,并且是监督机器学习算法的简单模型。 本质上是关于为观察到的数据拟合一条线。 我们将从解释监督学习和线性回归开始我们的旅程。 然后,我们将分析线性回归的关键概念,例如自变量和因变量,超参数,损失和误差函数以及随机梯度下降。 对于建模,我们将使用与上一章相同的数据集。
本章将介绍以下主题:
- 监督学习和线性回归
- 自变量和因变量
- 超参数
- 损失和误差函数
- 为单个变量实现我们的算法
- 计算随机梯度下降
- 使用线性回归建模房价
监督学习和线性回归
机器学习使计算机系统无需显式编程即可学习。 监督学习是最常见的机器学习类型之一。 监督学习由一组不同的算法组成,这些算法提出学习问题并通过使用历史数据映射输入和输出来解决它们。 该算法分析输入和相应的输出,然后将它们链接在一起以找到关系(学习)。 最后,对于新的给定数据集,它将使用此学习来预测输出。
为了区分监督学习和非监督学习,我们可以考虑基于输入/输出的建模。 在监督学习中,将对计算机系统的每组输入数据使用标签进行监督。 在无监督学习中,计算机系统将仅使用没有任何标签的输入数据。
例如,假设我们有 100 万张猫和狗的照片。 在监督学习中,我们标记输入数据并声明给定的照片是猫还是狗。 假设每张照片(输入数据)有 20 个特征。 标有照片的计算机系统将知道照片是猫还是狗(输出数据)。 当我们向计算机系统显示一张新照片时,它将通过分析新照片的 20 个特征来确定它是猫还是狗,并根据其先前的学习进行预测。 在无监督学习中,我们将只拥有 100 万张猫和狗的照片,而没有任何标签说明是猫还是狗的照片,因此该算法将在没有我们监督的情况下通过分析其特征来对数据进行聚类。 聚类完成后,会将新照片输入到无监督学习算法中,系统会告诉我们该照片属于哪个聚类。
在这两种情况下,系统都将具有简单或复杂的决策算法。 唯一的区别是是否有任何初始监督。 监督学习方法的概述方案如下:
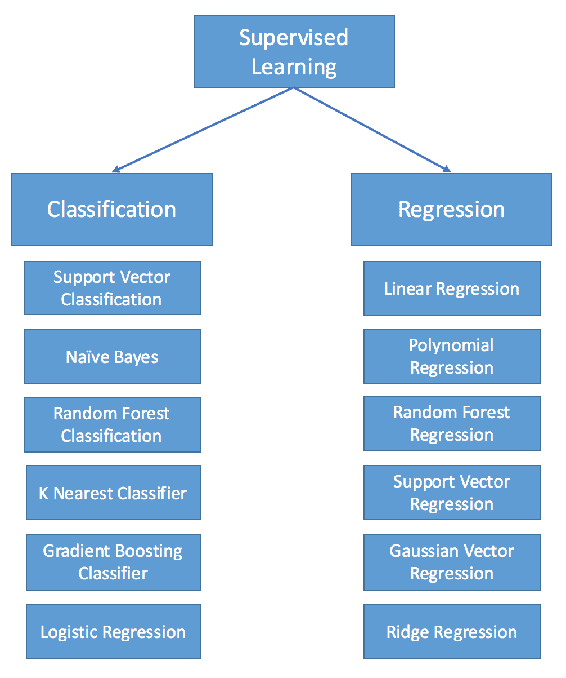
监督学习可以分为分类和回归两种类型,如上图所示。 分类模型预测标签。 例如,可以将前面的示例视为监督分类问题。 为了执行分类,我们需要训练分类算法,例如支持向量分类器(SVC),随机森林, K 近邻(KNN),依此类推。 基本上,分类器是指用于对数据进行分类(分类)的算法。
当我们的目标变量是分类变量时使用分类方法,而当我们的目标变量是连续变量时,则应用回归模型,因为目标是预测数值而不是类别。
考虑一下我们在上一章中使用的数据集:波士顿房屋价格数据集。 在该数据集中,我们的目的是对特征值进行统计分析,因为我们需要了解特征值的分布方式,其基本统计量以及之间的相互关系。 最后,我们想知道每个特征如何导致房价上涨。 它对正面,负面还是根本没有影响? 如果特征 x 与房屋价格 A 之间存在潜在的影响(关系),则该关系的强弱是多少?
我们试图通过建立模型来预测具有给定特征的房价来回答这些问题。 结果,在为模型提供新特征后,我们期望模型将输出变量生成为连续值(150k,120,154 美元等)。 让我们看一个非常基本的工作流程:
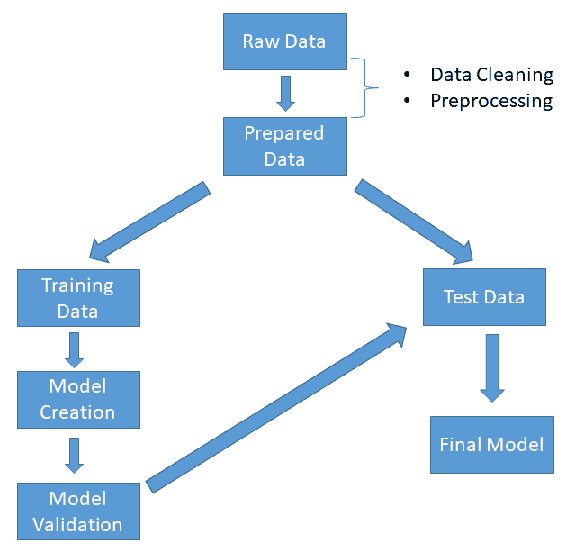
如上图所示,分析从为模型准备数据开始。 在此阶段,我们应该清理数据,处理缺失的值,并提取将要使用的特征。 数据干净后,我们应该将其分为训练数据和测试数据两部分,以测试模型的性能。
模型验证中的重要部分是过拟合的概念。 用外行的术语来说,过度拟合意味着从训练数据集中学到太多,因此我们的模型过度拟合并为训练数据集产生近乎完美的结果。 但是,对于从未见过的数据,它的灵活性不足以产生良好的结果,因此无法很好地泛化。
可以将数据集分为训练,验证(强烈推荐)和测试数据集来解决此问题。 训练数据是算法最初学习算法参数(权重)并在其中将误差最小化的地方建立模型的地方。 当您有几种算法并且需要调整超参数时,或者当算法中有许多参数并且需要调整参数时,平移数据集非常有用。 测试数据集用于性能评估。
简而言之,您可以使用训练数据来训练算法,然后在验证数据集中微调算法的参数或权重,最后一步,在测试数据集中测试调整后的算法的性能。
与过度拟合相反的情况是欠拟合,这意味着该算法从数据中学习得更少,并且我们的算法与我们的观察结果不太吻合。 让我们以图形方式查看过度拟合,欠拟合和最佳拟合的样子:
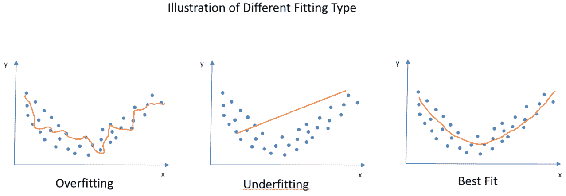
您可能已经注意到,在上图中,即使过度拟合看起来非常合适,它也会生成一个回归线,该回归线对于该数据集非常独特,并且无法正确捕获特征。 第二个图,即欠拟合图,实际上无法捕获数据的形状。 当我们的数据是非线性的时,它没有从中学习并产生了线性回归线。 第三个图是我们的最佳拟合图,拟合得很好,掌握了分布特征并产生了一条曲线。 我们可以预期,对于此数据集的延续,它不会有令人失望的性能指标。
在本章中,我们将使用线性回归作为有监督的学习方法。 我们将首先解释非常重要的概念,例如自变量和因变量,超参数以及损失和误差函数。 我们还将介绍线性回归的实际示例。 在下一章中,我们将介绍线性回归模型的最重要组成部分:独立变量和因变量。
自变量和因变量
正如我们在前面的小节中提到的,线性回归用于基于其他变量来预测变量的值。 我们正在研究输入变量X与输出变量Y之间的关系。
在线性回归中,因变量是我们要预测的变量。 之所以称其为因变量,是因为线性回归背后的假设。 该模型假设这些变量取决于方程另一侧的变量,这些变量称为独立变量。
在简单回归模型中,模型将解释因变量如何基于自变量而变化。
例如,假设我们要分析基于给定产品的价格变化如何影响销售值。 如果您仔细阅读此句子,则可以轻松检测出我们的因变量和自变量。 在我们的示例中,我们假设销售值受价格变化的影响,换句话说,销售值取决于产品的价格。 结果,销售值是从属值,价格是独立的值。 这不一定意味着给定产品的价格不依赖于任何东西。 当然,它取决于许多因素(变量),但是在我们的模型中,我们假设价格是给定的,并且给定的价格会改变销售值。 线性回归线的公式如下:
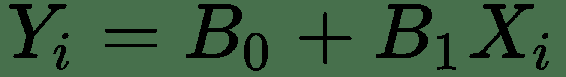
哪里:
Yi =估计值或因变量
B0 =截距
B1 =斜率
Xi =自变量或探索变量:
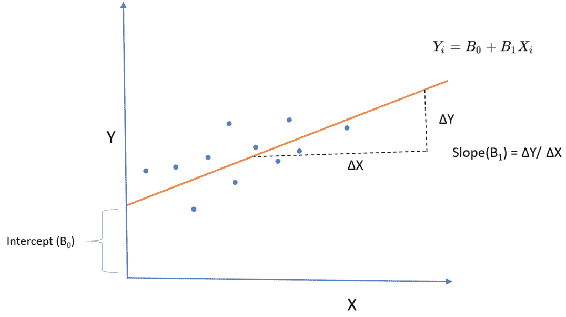
线性回归线的斜率(B1)实际上显示了这两个变量之间的关系。 假设我们将斜率计算为 0.8。 这意味着自变量增加 1 个单位可能会使估计值增加 0.8 个单位。 前面的线性回归线仅生成估计,这意味着它们仅是给定X的Y的预测。 如下图所示,每个观测值和线性线之间有一段距离。 该距离称为误差,这是预期的,在回归线拟合和模型评估中也非常重要:
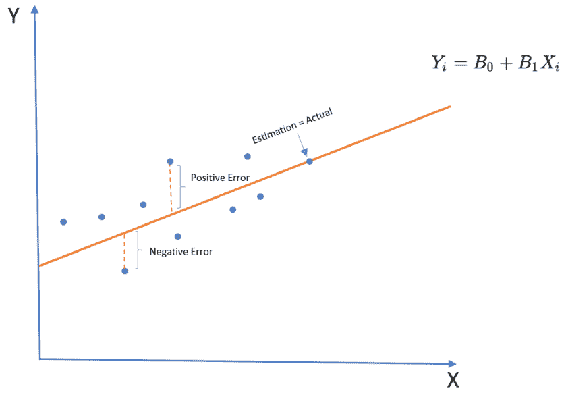
拟合线性回归线的最常见方法是使用最小二乘方法。 该方法通过最小化这些误差的平方和来拟合回归线。 计算公式如下:
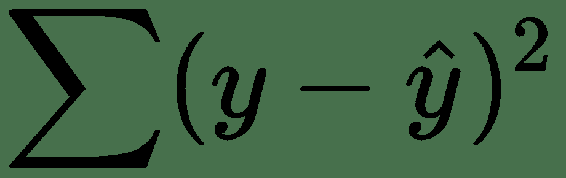
这些误差均方根的原因是我们不希望负误差和正误差彼此抵消。 在模型评估中,使用 R 平方,F 检验和均方根误差(RMSE)。 他们都使用平方和(SST)和平方和误差(SSE)作为基本度量。 如您所见,在 SSE 中,我们再次计算预测值和实际值之间的差,取平方并求和,以评估回归线对数据的拟合程度。
如前所述,最小二乘方法旨在最小化平方误差(残差),并找到最适合数据点的斜率和截距值。 由于这是一种封闭形式的解决方案,因此您可以轻松地手动计算它,以便在后台查看此方法的作用。 让我们使用一个包含少量数据集的示例:
| 牛奶消耗量(每周升) | 身高 |
|---|---|
| 14 | 175 |
| 20 | 182 |
| 10 | 170 |
| 15 | 185 |
| 12 | 164 |
| 15 | 173 |
| 22 | 181 |
| 25 | 193 |
| 12 | 160 |
| 13 | 165 |
假设我们有 10 个观察值,如上表所示,用于每周食用牛奶和食用牛奶的人的身高值。 如果我们绘制这些数据,我们可以看到每日牛奶消耗量与身高之间存在正相关:
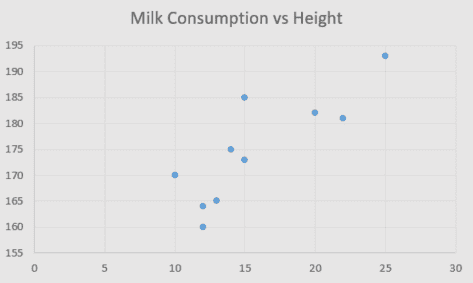
现在,我们要使用最小二乘法拟合线性回归线,该方法通过对斜率和截距使用以下公式来完成:
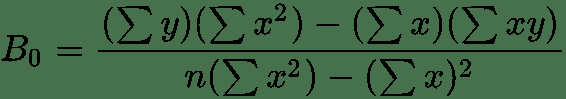
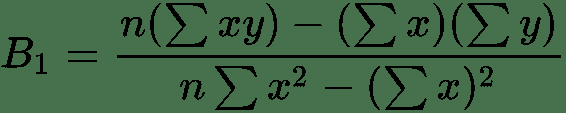
然后,我们需要创建一个表格来帮助我们进行计算,例如x,y,xy,x^2和y^2的总和:
x(牛奶消耗量) |
y(高度) |
xy |
x^2 |
y^2 |
|
|---|---|---|---|---|---|
| 1 | 14 | 175 | 2,450 | 196 | 30,625 |
| 2 | 20 | 182 | 3,640 | 400 | 33,124 |
| 3 | 10 | 170 | 1,700 | 100 | 28,900 |
| 4 | 15 | 185 | 2,775 | 225 | 34,225 |
| 5 | 12 | 164 | 1,968 | 144 | 26,896 |
| 6 | 15 | 173 | 2,595 | 225 | 29,929 |
| 7 | 22 | 181 | 3,982 | 484 | 32,761 |
| 8 | 25 | 193 | 4,800 | 625 | 37,249 |
| 9 | 12 | 160 | 1,920 | 144 | 25,600 |
| 10 | 13 | 165 | 2,145 | 169 | 27,225 |
| ∑ | 158 | 1,748 | 27,975 | 2,712 | 306,534 |
B0 = (1748*2712) - (158*27975) / (10*2712) - (158)^2 = 320526/2156 = 148.66
B1 = (10*27975) - (158*1748) / (10*2712) - (158)^2 = 1.65
然后,我们可以将回归线公式如下:
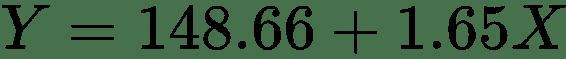
在本小节中,我们提到了自变量和因变量,并介绍了线性回归线和拟合方法。 在下一节中,我们将介绍超参数,这些参数在回归模型调整中非常有用。
超参数
在开始之前,也许最好解释一下为什么我们称它们为超参数而不是参数。 在机器学习中,可以从数据中学习模型参数,这意味着在训练模型时,您可以拟合模型的参数。 另一方面,我们通常在开始训练模型之前先设置超参数。 为了举例说明,您可以将回归模型中的系数视为模型参数。 以超参数为例,我们可以说许多不同模型中的学习率或 K 均值聚类中的聚类数(k)。
另一个重要的事情是模型参数和超参数之间的关系,以及它们如何塑造我们的机器学习模型,换句话说,就是我们模型的假设。 在机器学习中,参数用于配置模型,此配置将为我们的数据集专门定制算法。 我们需要处理的是如何优化超参数。 另外,如上所述,可以在验证期间执行该优化。 在许多情况下,优化超参数将带来性能提升。
您还可以将超参数视为模型参数之上的高级参数。 想象一下您使用无监督学习的 K 均值聚类的情况。 如果您使用误差的群集号(K)作为超参数,则可以确保您的数据不适合。
现在,您应该问的是,如果在训练模型之前手动设置超参数,我们该如何调整它们。 有几种方法可以调整超参数。 此优化的底线是使用一组不同的超参数测试算法,并在选择性能更好的超参数集之前针对每种情况计算误差函数或损失函数。
在本节中,我们简要介绍了参数,超参数及其差异。 在下一节中,我们将介绍损失和误差函数,这对于超参数优化非常重要。
损失和误差函数
在前面的小节中,我们解释了有监督和无监督的学习。 无论使用哪种机器学习算法,我们的主要挑战都是关于优化的问题。 在优化函数中,我们实际上是在尝试使损失函数最小化。 设想一下您试图优化每月储蓄的情况。 在关闭状态下,您要做的就是最小化支出,换句话说,将损失函数最小化。
建立损失函数的一种非常常见的方法是从预测值与实际值之差开始。 通常,我们尝试估计模型的参数,然后进行预测。 我们可以用来评估我们的预测水平的主要度量包括计算实际值之间的差:
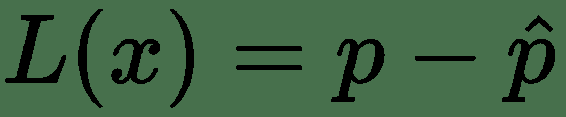
在不同的模型中,使用了不同的损失函数。 例如,您可以在回归模型中使用均方误差,但是将其用作分类模型的损失函数可能不是一个好主意。 例如,您可以按以下方式计算均方误差:
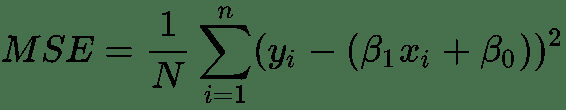
其中回归模型如下:
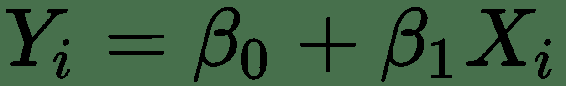
有许多不同的损失函数可用于不同的机器学习模型。 以下是一些重要的说明,并简要说明了它们的用法:
| 损失函数 | 解释 |
|---|---|
| 交叉熵 | 这用于分类模型,其中模型的输出为 0-1 之间的概率。 这是对数损失函数,也称为对数损失。 当理想的模型的概率接近 1.0 时, 交叉熵损失降低。 |
| MAE(L1) | 计算误差绝对值的均值。 由于它仅使用绝对值,因此不会将较大误差的权重放大。 当较大误差与较小误差相比可以容忍时,这很有用。 |
| MSE(L2) | 计算误差的平方根的均值。 放大较大误差的权重。 当不希望出现较大误差时,这很明智。 |
| Hinge | 这是用于线性分类器模型(例如支持向量机)的损失函数。 |
| Huber | 这是回归模型的损失函数。 它与 MSE 非常相似,但对异常值不敏感。 |
| Kullback-Leibler | Kullback-Leibler 散度衡量两个概率分布之间的差异 。 KL 损失函数在 T 分布随机邻居嵌入算法中大量使用。 |
在机器学习算法中,损失函数在更新变量权重时至关重要。 假设您使用反向传播训练神经网络。 在每次迭代中,都会计算出总误差。 然后,权重被更新以便最小化总误差。 因此,使用正确的损失函数会直接影响您的机器学习算法的性能,因为它直接影响模型参数。 在下一章中,我们将从住房数据中的单个变量开始简单的线性回归。
使用梯度下降的单变量线性回归
在本小节中,我们将为波士顿住房数据集实现单变量线性回归,该数据已在上一章中用于探索性数据分析。 在拟合回归线之前,让我们导入必要的库并按以下方式加载数据集:
In [1]: import numpy as np
import pandas as pd
from sklearn.cross_validation import train_test_split
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
%matplotlib inline
In [2]: from sklearn.datasets import load_boston
dataset = load_boston()
samples , label, feature_names = dataset.data, dataset.target, dataset.feature_names
In [3]: bostondf = pd.DataFrame(dataset.data)
bostondf.columns = dataset.feature_names
bostondf['Target Price'] = dataset.target
bostondf.head()
Out[3]: CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT Target Price
0 0.00632 18.0 2.31 0.0 0.538 6.575 65.2 4.0900 1.0 296.0 15.3 396.90 4.98 24.0
1 0.02731 0.0 7.07 0.0 0.469 6.421 78.9 4.9671 2.0 242.0 17.8 396.90 9.14 21.6
2 0.02729 0.0 7.07 0.0 0.469 7.185 61.1 4.9671 2.0 242.0 17.8 392.83 4.03 34.7
3 0.03237 0.0 2.18 0.0 0.458 6.998 45.8 6.0622 3.0 222.0 18.7 394.63 2.94 33.4
4 0.06905 0.0 2.18 0.0 0.458 7.147 54.2 6.0622 3.0 222.0 18.7 396.90 5.33 36.2
与上一章相比,我们使用 Pandas 数据帧代替了 numpy 数组,以便向您展示数据帧的用法,因为它也是一个非常方便的数据结构。 从技术上讲,在大多数情况下,如果仅将数值存储在 numpy 数组或 Pandas 数据帧中,则没有任何区别。 让我们将目标值添加到数据框中,并使用散点图查看RM函数与目标值之间的关系:
In [4]: import matplotlib.pyplot as plt
bostondf.plot(x='RM', y='Target Price', style= 'o')
plt.title('RM vs Target Price')
plt.ylabel('Target Price')
plt.show()
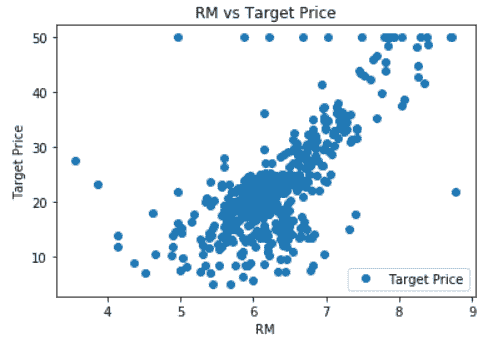
从该图可以看出,每个住宅的平均房间数(RM)与房价之间存在正相关,正如预期的那样。 现在,我们将看到这种关系的强度,并尝试使用这种关系来预测房价。
想象一下,您对线性回归的了解非常有限。 假设您只是熟悉方程式,但不知道误差函数是什么,为什么我们需要迭代,什么是梯度下降,以及为什么要在线性回归模型中使用它。 在这种情况下,您要做的就是简单地开始传递系数的一些初始值,并在计算预测值之前截取方程。
在计算了几个预测值之后,您可以将它们与实际值进行比较,看看您与实际情况有多远。 下一步将是更改系数或截距,或者同时进行这两项操作,以查看是否可以使结果更接近实际值。 如果您对此过程感到满意,这就是我们的算法将以更智能的方式进行的操作。
为了更好地理解线性回归模型步骤,我们将代码分成几个块。 首先,让我们创建一个函数,该函数作为回归线的结果返回预测值:
In [5]: def prediction(X, coefficient, intercept):
return X*coefficient + intercept
前面的函数计算线性回归模型如下:
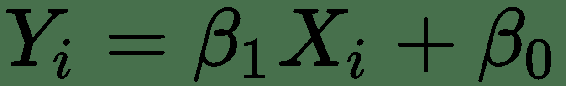
然后,我们需要一个成本函数,该函数将在每次迭代中进行计算。 作为cost_function,我们将使用均方误差,它是预测值与实际值之间总平方差的平均值:
In [6]: def cost_function(X, Y, coefficient, intercept):
MSE = 0.0
for i in range(len(X)):
MSE += (Y[i] - (coefficient*X[i] + intercept))**2
return MSE / len(X)
我们的最后一个代码块将用于更新权重。 当我们讨论权重时,不仅涉及自变量的系数,还涉及截距。 拦截也称为偏差。 为了逻辑上更新权重,我们需要一种迭代优化算法,该算法可以找到给定函数的最小值。 在此示例中,我们将使用梯度下降方法来最小化每次迭代中的损失函数。 让我们一步一步地发现梯度下降的作用。
首先,我们应该初始化权重(截距和系数)并计算均方误差。 然后,我们需要计算梯度,这意味着查看当改变权重时均方误差如何变化。
为了以更智能的方式更改权重,我们需要了解我们必须更改系数和截距的方向。 这意味着我们在更改权重时应计算误差函数的梯度。 我们可以通过对系数和截距采用损失函数的偏导数来计算梯度。
在单变量线性回归中,我们只有一个系数。 在计算偏导数之后,该算法将调整权重并重新计算均方误差。 此过程将重复进行,直到更新的权重不再减小均方误差为止:
In [7]: def update_weights(X, Y, coefficient, intercept, learning_rate):
coefficient_derivative = 0
intercept_derivative = 0
for i in range(len(X)):
coefficient_derivative += -2*X[i] * (Y[i] - (coefficient*X[i] + intercept))
intercept_derivative += -2*(Y[i] - (coefficient*X[i] + intercept))
coefficient -= (coefficient_derivative / len(X)) * learning_rate
intercept -= (intercept_derivative / len(X)) * learning_rate
return coefficient, intercept
前面的代码块定义了更新权重的函数,然后返回更新的系数并进行拦截。 此函数中的另一个重要参数是learning_rate。 学习速度将决定变化的幅度:
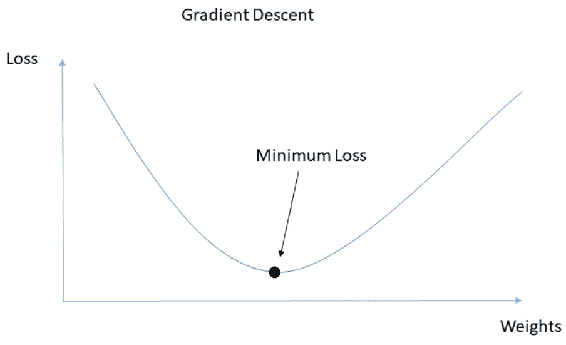
在上图中,您可以看到我们的损失函数为x = y^2的形状,因为它是平方误差的总和。 通过梯度下降,我们试图找到最小损耗,如图所示,其中偏导数非常接近零。 如前所述,我们通过初始化权重来开始算法,这意味着我们从远离最小值的点开始。 在每次迭代中,我们将更新权重,从而减少损失。 这意味着给定足够的迭代次数,我们将收敛到全局最小值。 学习速度将决定这种融合发生的速度。
换句话说,当我们更新权重时,高学习率看起来就像是从一个点到另一个点的巨大跳跃。 低学习率将慢慢接近全局最小值(所需的最小损失点)。 由于学习率是一个超参数,因此我们需要在运行它之前进行设置:
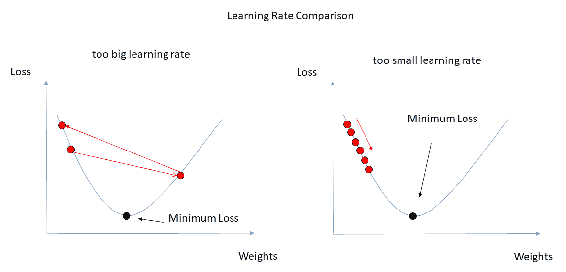
那么,我们需要设定学习率的大还是小? 答案是我们应该找到最佳速率。 如果我们设定较高的学习率,我们的算法将超出最小值。 我们很容易错过最小值,因为这些跳跃永远不会让我们的算法收敛到全局最小值。 另一方面,如果我们将学习率设置得太小,则可能需要进行大量迭代才能收敛。
具有先前的代码块,是时候编写主函数了。 主函数应遵循我们前面讨论的流程:
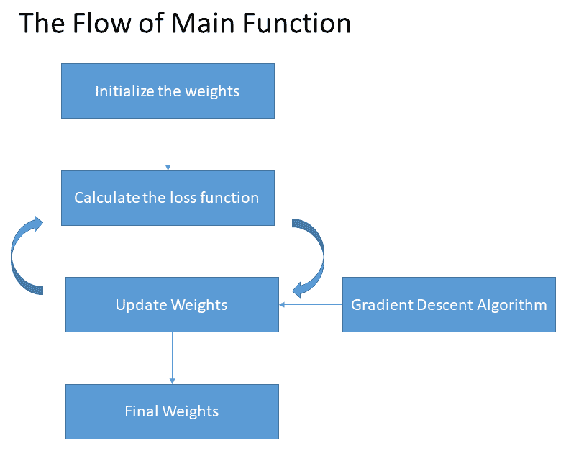
然后,主函数的代码块应如下所示:
In [8]: def train(X, Y, coefficient, intercept, LearningRate, iteration):
cost_hist = []
for i in range(iteration):
coefficient, intercept = update_weights(X, Y, coefficient, intercept, learning_cost = cost_function(X, Y, coefficient, intercept)
cost_hist.append(cost)
return coefficient, intercept, cost_hist
现在,我们已经定义了所有代码块,并且可以运行单变量模型了。 在运行train()函数之前,我们需要设置系数和截距的超参数和初始值。 您可以创建变量,设置值,然后将这些变量作为函数的参数,如下所示:
In [9]: learning_rate = 0.01
iteration = 10001
coefficient = 0.3
intercept = 2
X = bostondf.iloc[:, 5:6].values
Y = bostondf.iloc[:, 13:14].values
coefficient, intercept, cost_history = train(X, Y, coefficient, intercept, learning_rate, iteration)
或者,可以在调用函数时将这些值作为关键字参数传递:
coefficient, intercept, cost_history = train(X, Y, coefficient, intercept = 2, learning_rate = 0.01, iteration = 10001)
我们的主函数将返回两个数组,这将为我们提供拦截和系数的最终值。 此外,主函数将返回损失值列表,这是每次迭代的结果。 这些是每次迭代中均方误差的结果。 拥有此列表以跟踪每次迭代中损耗的变化非常有用:
In [10]: coefficient
Out[10]: array([8.57526661])
In [11]: intercept
Out[11]: array([-31.31931428])
In [12]: cost_history
array([54.18545801]),
array([54.18036786]),
array([54.17528017]),
array([54.17019493]),
array([54.16511212]),
array([54.16003177]),
array([54.15495385]),
array([54.14987838]),
array([54.14480535]),
array([54.13973476]),
array([54.13466661]),
array([54.12960089]),
array([54.12453761]),
array([54.11947677]),
array([54.11441836]),
array([54.10936238]),
array([54.10430883]),
...]
从系数值中可以看出,RM的每增加 1 单位,住房价格就会升至 8,575 美元左右。 现在,让我们通过将计算出的截距和系数注入回归公式中来计算预测值。 然后,我们可以绘制线性回归线并查看其如何拟合我们的数据:
In [13]: y_hat = X*coefficient + intercept
plt.plot(X, Y, 'bo')
plt.plot(X, y_hat)
plt.show()
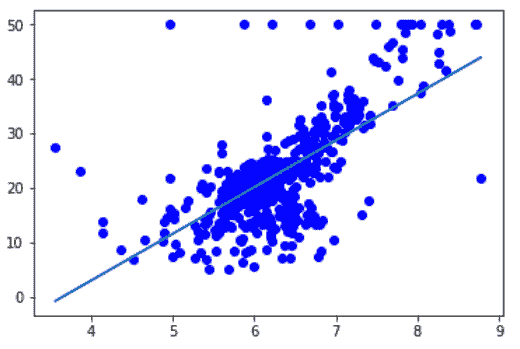
在本节中,我们通过选择一个变量来应用单变量模型。 在以下小节中,我们将通过在模型中添加更多自变量来执行多元线性回归模型,这意味着我们将有多个系数可进行优化以实现最佳拟合。
使用线性回归建模房价
在本节中,我们将对同一数据集执行多元线性回归。 与上一节相反,我们将使用 sklearn 库向您展示执行线性回归模型的几种方法。 在开始线性回归模型之前,我们将使用trimboth()方法从两侧按比例修剪数据集。 通过这样做,我们将消除异常值:
In [14]: import numpy as np
import pandas as pd
from scipy import stats
from sklearn.cross_validation import train_test_split
from sklearn.linear_model import LinearRegression
In [15]: from sklearn.datasets import load_boston
dataset = load_boston()
In [16]: samples , label, feature_names = dataset.data, dataset.target, dataset.feature_names
In [17]: samples_trim = stats.trimboth(samples, 0.1)
label_trim = stats.trimboth(label, 0.1)
In [18]: print(samples.shape)
print(label.shape)
(506, 13)
(506,)
In [19]: print(samples_trim.shape)
print(label_trim.shape)
(406, 13)
(406,)
正如您在前面的代码块中看到的那样,由于我们将左右数据修剪了 10% ,每个属性和标签列的样本量从 506 减少到 406:
In [20]: from sklearn.model_selection import train_test_split
samples_train, samples_test, label_train, label_test = train_test_split(samples_trim, In [21]: In [21]: print(samples_train.shape)
print(samples_test.shape)
print(label_train.shape)
print(label_test.shape)
(324, 13)
(82, 13)
(324,)
(82,)
In [22]: regressor = LinearRegression()
regressor.fit(samples_train, label_train)
Out[22]: LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
In [23]: regressor.coef_
Out[23]: array([ 2.12924665e-01, 9.16706914e-02, 1.04316071e-01, -3.18634008e-14,
5.34177385e+00, -7.81823481e-02, 1.91366342e-02, 2.81852916e-01,
3.19533878e-04, -4.24007416e-03, 1.94206366e-01, 3.96802252e-02,
3.81858253e-01])
In [24]: regressor.intercept_
Out[24]: -6.899291747292615
然后,我们使用train_test_split()方法将数据集拆分为训练和测试。 这种方法在机器学习算法中非常普遍。 您将数据分为两组,然后让模型训练(学习),然后再使用数据的另一部分测试模型。 使用这种方法的原因是为了减少验证模型时的偏差。 每个系数代表当我们将这些样本增加一个单位时,预期目标值将改变多少:
In [25]: label_pred = regressor.predict(samples_test)
In [26]: plt.scatter(label_test, label_pred)
plt.xlabel("Prices")
plt.ylabel("Predicted Prices")
plt.title("Prices vs Predicted Prices")
plt.axis("equal")
Out[26]: (11.770143369175626, 34.22985663082437, 10.865962968036989, 34.20549738482051)
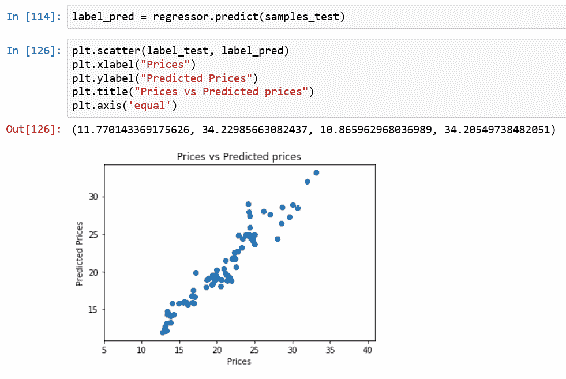
让我们在前面的代码块中测试我们的模型。 为了在数据集上运行我们的模型,我们可以使用predict()方法。 此方法将在模型上运行给定的数据集并返回结果。 理想情况下,我们期望该点以x = y线形分布,换言之,例如具有 45 度角的直线。 这是一个完美的一对一匹配预测。 我们不能说我们的预测是完美的,但是仅通过查看散点图,我们可以得出结论,该预测不是一个坏的预测。 我们可以查看有关模型性能的两个重要指标,如下所示:
In [27]: from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
mse = mean_squared_error(label_test, label_pred)
r2 = r2_score(label_test, label_pred)
print(mse)
print(r2)
2.032691267250478
0.9154474686142619
第一个是均方误差。 您可能已经注意到,当我们在模型中添加更多自变量时,它会大大降低。 第二个是 R 方,它是确定系数,或者换句话说,是回归得分。 确定系数可以解释您的自变量解释了因变量有多少方差。 在我们的模型中,结果为 0.91,这说明我们的 13 个特征可以解释 91% 的房价差异。 如您所见,sklearn 具有许多有用的线性回归内置函数,这些函数可以加快模型构建过程。 另一方面,您也可以仅使用 numpy 轻松构建线性回归模型,这可以为您提供更大的灵活性,因为您可以控制算法的每个部分。
总结
线性回归是对连续变量之间的关系进行建模的最常用技术之一。 这种方法的应用在工业上非常广泛。 我们开始对本书的一部分进行线性回归建模,这不仅是因为它非常流行,还因为它是一种相对简单的技术,并且包含了几乎每种机器学习算法都具有的大多数要素。
在本章中,我们了解了监督学习和无监督学习,并使用波士顿房屋数据集建立了线性回归模型。 我们谈到了不同的重要概念,例如超参数,损失函数和梯度下降。 本章的主要目的是为您提供足够的知识,以便您可以建立和调整线性回归模型并逐步了解它的作用。 我们研究了两个使用单变量和多元线性回归的实际案例。 您还体验了 numpy 和 sklearn 在线性回归中的用法。 我们强烈建议您对不同的数据集进行进一步练习,并检查更改超参数时结果如何变化。
在下一章中,我们将学习聚类方法,并通过批发分销商数据集上的示例进行实践。
五、使用 NumPy 对批发分销商的客户进行聚类
通过查看 NumPy 在各种使用案例中的使用,您肯定可以提高自己的技能。 本章介绍的分析类型与迄今为止所见不同。 聚类是一种无监督的学习技术,用于理解和捕获数据集中的各种形式。 由于您没有标签来监督您的学习算法,因此在很多情况下,可视化是关键,这就是为什么您也会看到各种可视化技术的原因。
在本章中,我们将介绍以下主题:
- 无监督学习和聚类
- 超参数
- 扩展简单算法来聚类批发分销商的客户
无监督学习和聚类
让我们用一个例子快速回顾一下监督学习。 在训练机器学习算法时,您可以通过提供标签来观察和指导学习。 考虑下面的数据集,其中每一行代表一个客户,每一列代表一个不同的特征,例如年龄,性别,收入,职业 ,任期和城市。 看看这个表:
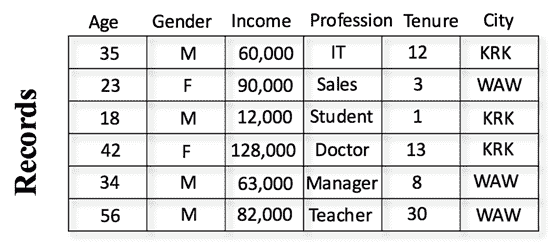
您可能需要执行不同类型的分析。 其中一项可能是预测哪些客户可能会离开,即客户流失分析。 为此,您需要根据每个客户的历史记录为其标记标签,以指示哪些客户已离开或留下,如下表所示:
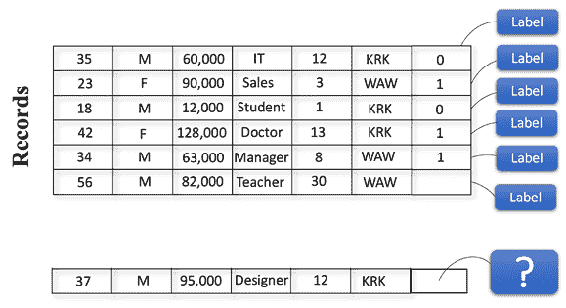
您的算法将根据客户的标签了解客户的特征。 算法将学习离开或留下的客户的特征,并且,当您希望根据这些特征为新客户评分时,算法将根据该学习进行预测。 这称为监督学习。
关于此数据集可能要问的另一个问题可能是:此数据集中存在多少个客户组,以便其组中的每个客户都与其他客户相似,而与属于其他组的客户不同。 流行的聚类算法(例如 K 均值)可以帮助您解决这一问题。 例如,一旦 K 均值将客户分配到不同的集群,则一个集群可以大体上包括 30 岁以下且以 IT 作为职业的客户,而另一个集群可以大体上包括 60 岁以上的客户并且职业为老师。 您无需标记数据集即可执行此分析,因为算法足以查看记录并确定它们之间的相似性。 由于没有监督,因此这种学习称为无监督学习。
进行此类分析时,首先可视化数据集会很有帮助。 您可以从可用的数据集开始构建您的处理和建模工作流程。 以下代码段显示了如何使用plotly可视化三维数据集。plotly是一个库,可让您绘制许多不同的交互式图表以进行探索性分析,并使数据探索更加容易。
首先,您需要使用以下代码段安装必要的库:
## Installing necessary libraries with pip
!pip install plotly --user
!pip install cufflinks -user
然后,使用以下代码导入必要的库:
## Necessary imports
import os
import sys
import numpy as np
import pandas
import matplotlib.pyplot as plt
%matplotlib inline
import plotly.plotly as py
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
import cufflinks as cf
import plotly.graph_objs as go
init_notebook_mode(connected=True)
sys.path.append("".join([os.environ["HOME"]]))
您将使用sklearn.datasets模块中可用的iris数据集,如下所示:
from sklearn.datasets import load_iris
iris_data = load_iris()
iris数据具有四个特征; 它们如下:
iris_data.feature_names
['sepal length (cm)',
'sepal width (cm)',
'petal length (cm)',
'petal width (cm)']
首先,让我们检查一下前两个特征:
x = [v[0] for v in iris_data.data]
y = [v[1] for v in iris_data.data]
创建一个trace,然后创建数据和图形,如下所示:
trace = go.Scatter(
x = x,
y = y,
mode = 'markers'
)
layout= go.Layout(
title= 'Iris Dataset',
hovermode= 'closest',
xaxis= dict(
title= 'sepal length (cm)',
ticklen= 5,
zeroline= False,
gridwidth= 2,
),
yaxis=dict(
title= 'sepal width (cm)',
ticklen= 5,
gridwidth= 2,
),
showlegend= False
)
data = [trace]
fig= go.Figure(data=data, layout=layout)
plot(fig)
如下图所示,这将为您提供以下输出:
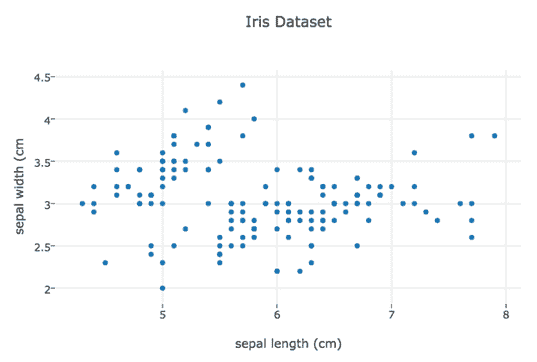
您可以继续查看其他变量,但是要更好地理解一张图表中要素之间的关系,可以使用scatterplot矩阵。 创建pandas.DataFrame与plotly结合使用会更加方便:
import pandas as pd
df = pd.DataFrame(iris_data.data,
columns=['sepal length (cm)',
'sepal width (cm)',
'petal length (cm)',
'petal width (cm)'])
df['class'] = [iris_data.target_names[i] for i in iris_data.target]
df.head()
使用plotly图形工厂,可以绘制scatterplot矩阵,如下所示:
import plotly.figure_factory as ff
fig = ff.create_scatterplotmatrix(df, index='class', diag='histogram', size=10, height=800, width=800)
plot(fig)
这将为您提供以下图表,如下图所示:
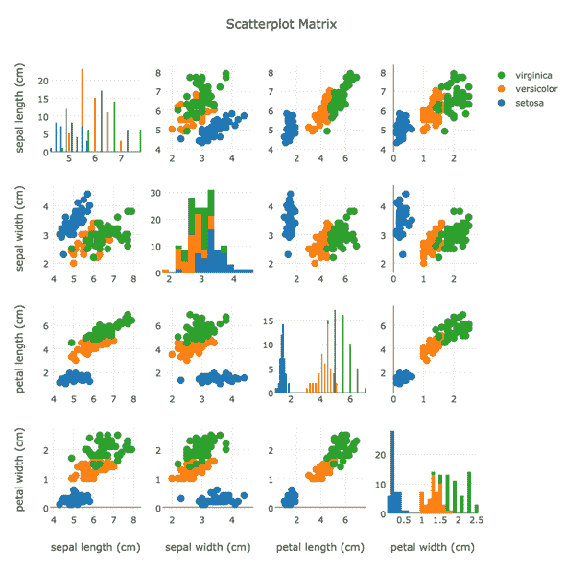
乍一看,花瓣长度,花瓣宽度和萼片长度似乎是建模的不错选择。 您可以通过以下代码使用 3D 图表进一步检查该数据集:
## Creating data for the plotly
trace1 = go.Scatter3d(
# Extracting data based on label
x=[x[0][0] for x in zip(iris_data.data, iris_data.target) if x[1] == 0],
y=[x[0][2] for x in zip(iris_data.data, iris_data.target) if x[1] == 0],
z=[x[0][3] for x in zip(iris_data.data, iris_data.target) if x[1] == 0],
mode='markers',
marker=dict(
size=12,
line=dict(
color='rgba(217, 217, 217, 0.14)',
width=0.5
),
opacity=0.8
)
)
trace2 = go.Scatter3d(
# Extracting data based on label
x=[x[0][0] for x in zip(iris_data.data, iris_data.target) if x[1] == 1],
y=[x[0][2] for x in zip(iris_data.data, iris_data.target) if x[1] == 1],
z=[x[0][3] for x in zip(iris_data.data, iris_data.target) if x[1] == 1],
mode='markers',
marker=dict(
color='rgb(#3742fa)',
size=12,
symbol='circle',
line=dict(
color='rgb(204, 204, 204)',
width=1
),
opacity=0.9
)
)
trace3 = go.Scatter3d(
# Extracting data based on label
x=[x[0][0] for x in zip(iris_data.data, iris_data.target) if x[1] == 2],
y=[x[0][2] for x in zip(iris_data.data, iris_data.target) if x[1] == 2],
z=[x[0][3] for x in zip(iris_data.data, iris_data.target) if x[1] == 2],
mode='markers',
marker=dict(
color='rgb(#ff4757)',
size=12,
symbol='circle',
line=dict(
color='rgb(104, 74, 114)',
width=1
),
opacity=0.9
)
)
data = [trace1, trace2, trace3]
### Layout settings
layout = go.Layout(
scene = dict(
xaxis = dict(
title= 'sepal length (cm)'),
yaxis = dict(
title= 'petal length (cm)'),
zaxis = dict(
title= 'petal width (cm)'),),
)
fig = go.Figure(data=data, layout=layout)
plot(fig)
这将为您提供以下交互式图表,如下图所示:
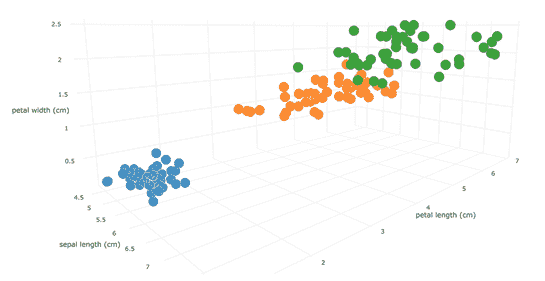
Interactive plotting of petal length, petal width, and sepal length
使用这些图表,您可以更好地理解数据并为建模做准备。
超参数
超参数可以被视为确定模型各种属性之一的高级参数,例如复杂性,训练行为和学习率。 这些参数自然与模型参数有所不同,因为它们需要在训练开始之前设置。
例如,K 均值或 K 最近邻中的 k 是这些算法的超参数。 K 均值中的 K 表示要找到的聚类数,K 最近邻中的 k 表示用于进行预测的最近记录数。
调整超参数是任何机器学习项目中提高预测性能的关键步骤。 有多种调优技术,例如网格搜索,随机搜索和贝叶斯优化,但这些技术不在本章范围之内。
让我们通过以下屏幕快照快速浏览 scikit-learn 库中的 K 均值算法参数:
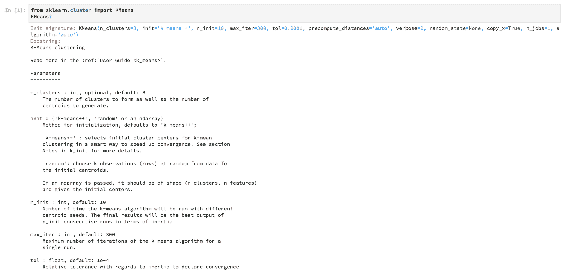
如您所见,有许多参数可以使用,并且至少应查看算法的函数签名,以查看运行算法之前的选项。
让我们一起玩吧。 基线模型将与样本数据一起使用,几乎具有默认设置,如下所示:
from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples=20, centers=3, n_features=3, random_state=42)
k_means = KMeans(n_clusters=3)
y_hat = k_means.fit_predict(X)
y_hat保留集群的成员身份信息,这与原始标签相同,如您在此处看到的:
y_hat
## array([0, 2, 1, 1, 1, 0, 2, 0, 0, 0, 2, 0, 1, 2, 1, 2, 2, 1, 0, 1],
dtype=int32)
y
## array([0, 2, 1, 1, 1, 0, 2, 0, 0, 0, 2, 0, 1, 2, 1, 2, 2, 1, 0, 1])
您可以使用不同的选项来查看它如何影响训练和预测。
损失函数
损失函数通过测量误差来帮助算法在训练过程中更新模型参数,这是预测性能的指标。 损失函数通常表示为:
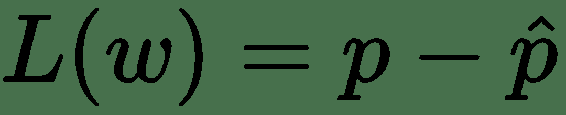
其中L测量预测值与实际值之间的差。 在训练过程中,此误差被最小化。 不同的算法具有不同的损失函数,迭代次数将取决于收敛条件。
例如,K 均值的损失函数使点与最接近的簇均值之间的平方距离最小化,如下所示:
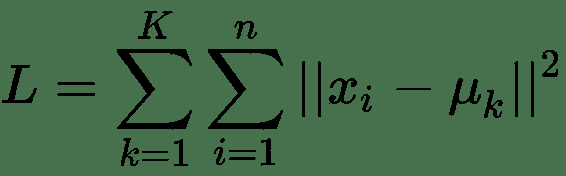
您将在以下部分中看到详细的实现。
为单个变量实现我们的算法
让我们为单个变量实现 K 均值算法。 您将从一维向量开始,该向量具有 20 条记录,如下所示:
data = [1,2,3,2,1,3,9,8,11,12,10,11,14,25,26,24,30,22,24,27]
trace1 = go.Scatter(
x=data,
y=[0 for x in data],
mode='markers',
name='Data',
marker=dict(
size=12
)
)
layout = go.Layout(
title='1D vector',
)
traces = [trace1]
fig = go.Figure(data=traces, layout=layout)
plot(fig)
如下图所示,将输出以下图表:
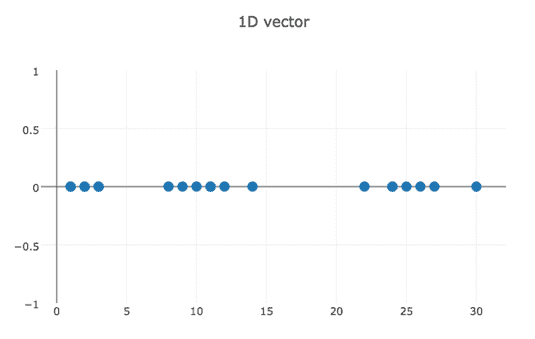
我们的目标是找到在数据中可见的3簇。 为了开始实施 K 均值算法,您需要通过选择随机索引来初始化集群中心,如下所示:
n_clusters = 3
c_centers = np.random.choice(X, n_clusters)
print(c_centers)
### [ 1 22 26]
接下来,您需要计算每个点与聚类中心之间的距离,因此请使用以下代码:
deltas = np.array([np.abs(point - c_centers) for point in X])
deltas
array([[ 7, 26, 10],
[ 6, 25, 9],
[ 5, 24, 8],
[ 6, 25, 9],
[ 7, 26, 10],
[ 5, 24, 8],
[ 1, 18, 2],
[ 0, 19, 3],
[ 3, 16, 0],
[ 4, 15, 1],
[ 2, 17, 1],
[ 3, 16, 0],
[ 6, 13, 3],
[17, 2, 14],
[18, 1, 15],
[16, 3, 13],
[22, 3, 19],
[14, 5, 11],
[16, 3, 13],
[19, 0, 16]])
现在,可以使用以下代码来计算集群成员资格:
deltas.argmin(1)
## array([0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1])
现在,您需要使用以下代码来计算记录和群集中心之间的距离:
c_centers = np.array([X[np.where(deltas.argmin(1) == i)[0]].mean() for i in range(3)])
print(c_centers)
### [ 3.625 25.42857143 11.6 ]
这是一次迭代; 您可以继续计算新的群集中心,直到没有任何改善为止。
您可以编写一个函数来包装所有这些功能,如下所示:
def Kmeans_1D(X, n_clusters, random_seed=442):
# Randomly choose random indexes as cluster centers
rng = np.random.RandomState(random_seed)
i = rng.permutation(X.shape[0])[:n_clusters]
c_centers = X[i]
# Calculate distances between each point and cluster centers
deltas = np.array([np.abs(point - c_centers) for point in X])
# Get labels for each point
labels = deltas.argmin(1)
while True:
# Calculate mean of each cluster
new_c_centers = np.array([X[np.where(deltas.argmin(1) == i)[0]].mean() for i in range(n_clusters)])
# Calculate distances again
deltas = np.array([np.abs(point - new_c_centers) for point in X])
# Get new labels for each point
labels = deltas.argmin(1)
# If there's no change in centers, exit
if np.all(c_centers == new_c_centers):
break
c_centers = new_c_centers
return c_centers, labels
c_centers, labels = Kmeans_1D(X, 3)
print(c_centers, labels)
### [11.16666667 25.42857143 2.85714286] [2 2 2 2 2 2 0 0 0 0 0 0 0 1 1 1 1 1 1 1]
让我们使用以下代码绘制集群中心的图表:
trace1 = go.Scatter(
x=X,
y=[0 for num in X],
mode='markers',
name='Data',
marker=dict(
size=12
)
)
trace2 = go.Scatter(
x = c_centers,
y = [0 for num in X],
mode='markers',
name = 'Cluster centers',
marker = dict(
size=12,
color = ('rgb(122, 296, 167)')
)
)
layout = go.Layout(
title='1D vector',
)
traces = [trace1, trace2]
fig = go.Figure(data=traces, layout=layout)
plot(fig)
看下图。 给定的代码将输出以下内容:
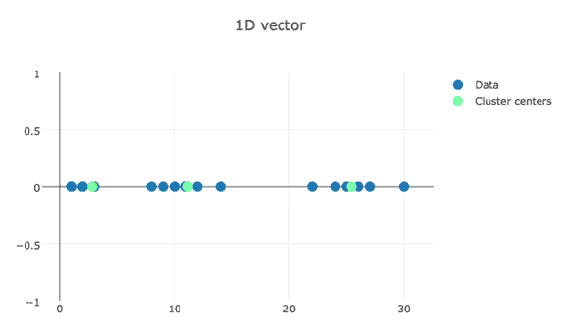
您可以清楚地看到,可以为每个元素分配一个聚类中心。
修改我们的算法
现在,您已经了解了单个变量的 K 均值内部,可以将该实现扩展到多个变量,并将其应用于更实际的数据集。
本节中使用的数据集来自 UCI 机器学习存储库,它包括批发分销商的客户信息。 有 440 个具有八项特征的客户。 在下面的列表中,前六个特征与相应产品的年度支出相关,第七个特征显示了购买该产品的渠道,第八个特征显示了该地区:
FRESHMILKGROCERYFROZENDETERGENTS_PAPERDELICATESSENCHANNELREGION
首先下载数据集并将其读取为numpy数组:
from numpy import genfromtxt
wholesales_data = genfromtxt('Wholesale customers data.csv', delimiter=',', skip_header=1)
您可以快速查看数据。 这里是:
print(wholesales_data[:5])
[[2.0000e+00 3.0000e+00 1.2669e+04 9.6560e+03 7.5610e+03 2.1400e+02
2.6740e+03 1.3380e+03]
[2.0000e+00 3.0000e+00 7.0570e+03 9.8100e+03 9.5680e+03 1.7620e+03
3.2930e+03 1.7760e+03]
[2.0000e+00 3.0000e+00 6.3530e+03 8.8080e+03 7.6840e+03 2.4050e+03
3.5160e+03 7.8440e+03]
[1.0000e+00 3.0000e+00 1.3265e+04 1.1960e+03 4.2210e+03 6.4040e+03
5.0700e+02 1.7880e+03]
[2.0000e+00 3.0000e+00 2.2615e+04 5.4100e+03 7.1980e+03 3.9150e+03
1.7770e+03 5.1850e+03]]
选中shape将显示行数和变量数,如下所示:
wholesales_data.shape
## (440, 8)
该数据集具有440个记录,每个记录都有8个特征。
通过使用以下代码来规范化数据集是一个好主意:
wholesales_data_norm = wholesales_data / np.linalg.norm(wholesales_data)
print(wholesales_data_norm[:5])
[[ 1\. 0\. 0.30168043 1.06571214 0.32995207 -0.46657183
0.50678671 0.2638102 ]
[ 1\. 0\. -0.1048095 1.09293385 0.56599336 0.08392603
0.67567015 0.5740085 ]
[ 1\. 0\. -0.15580183 0.91581599 0.34441798 0.3125889
0.73651183 4.87145892]
[ 0\. 0\. 0.34485007 -0.42971408 -0.06286202 1.73470839
-0.08444172 0.58250708]
[ 1\. 0\. 1.02209184 0.3151708 0.28726 0.84957326
0.26205579 2.98831445]]
您可以使用以下代码将数据集读取到pandas.DataFrame中:
import pandas as pd
df = pd.DataFrame(wholesales_data_norm,
columns=['Channel',
'Region',
'Fresh',
'Milk',
'Grocery',
'Frozen',
'Detergents_Paper',
'Delicatessen'])
df.head(10)
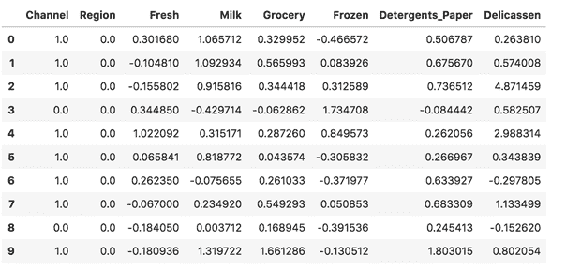
让我们创建一个scatterplot矩阵以更仔细地查看数据集。 看一下代码:
fig = ff.create_scatterplotmatrix(df, diag='histogram', size=7, height=1200, width=1200)
plot(fig)
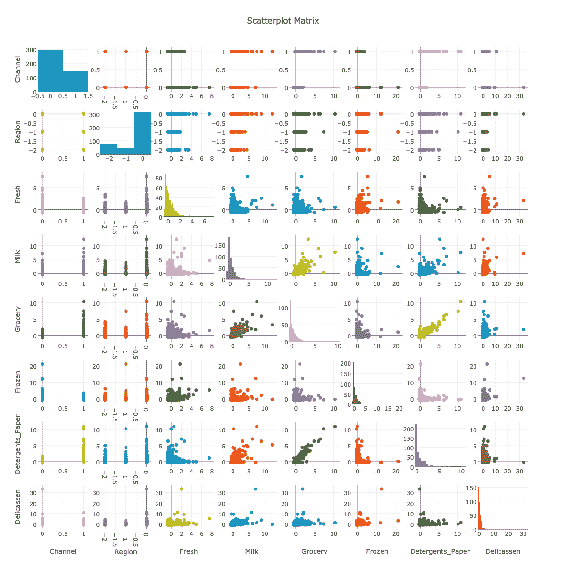
您还可以通过运行以下命令来检查要素之间的相关性:
df.corr()
这将为您提供一个关联表,如下所示:
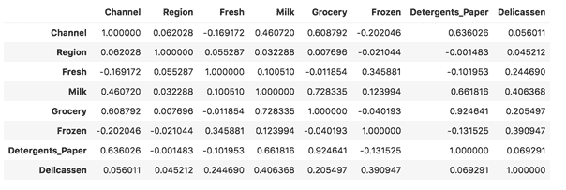
您还可以使用seaborn热图,如下所示:
import seaborn as sns; sns.set()
ax = sns.heatmap(df.corr(), annot=True)
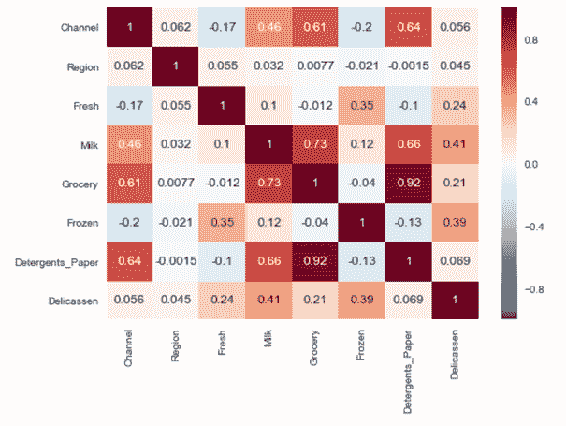
Correlations between the features
您可以看到特征之间存在一些很强的相关性,例如Grocery和Detergents_Paper之间的相关性。
让我们使用以下代码绘制Grocery,Detergents_Paper和Milk三个特征:
## Creating data for the plotly
trace1 = go.Scatter3d(
# Extracting data based on label
x=df['Grocery'],
y=df['Detergents_Paper'],
z=df['Milk'],
mode='markers',
marker=dict(
size=12,
line=dict(
color='rgba(217, 217, 217, 0.14)',
width=0.5
),
opacity=0.8
)
)
### Layout settings
layout = go.Layout(
scene = dict(
xaxis = dict(
title= 'Grocery'),
yaxis = dict(
title= 'Detergents_Paper'),
zaxis = dict(
title= 'Milk'),),
)
data = [trace1]
fig = dict(data=data, layout=layout)
plot(fig)
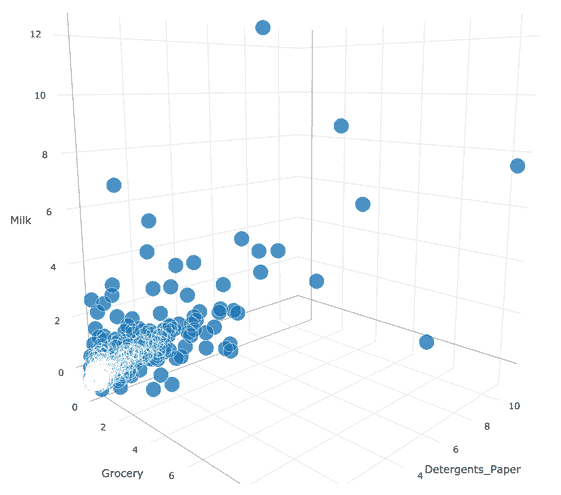
现在,您将继续扩展已为更高维度实现的 K 均值算法。 首先,您可以从数据集中删除Channel和Region,如下所示:
df = df[[col for col in df.columns if col not in ['Channel', 'Region']]]
df.head(10)
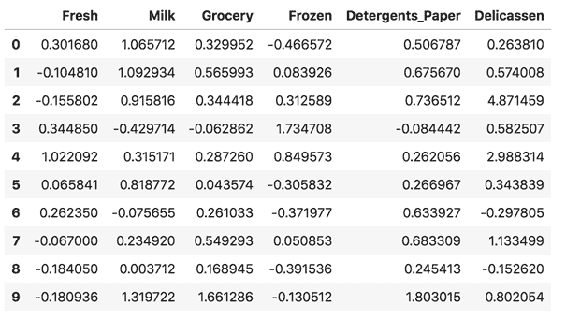
在实现方面,您还可以使用np.linalg.norm来计算距离,这实际上取决于您使用哪种距离函数。 另一个替代方法是scipy.spatial中的distance.euclidean,如下所示:
def Kmeans_nD(X, n_clusters, random_seed=442):
# Randomly choose random indexes as cluster centers
rng = np.random.RandomState(random_seed)
i = rng.permutation(X.shape[0])[:n_clusters]
c_centers = X[i]
# Calculate distances between each point and cluster centers
deltas = np.array([[np.linalg.norm(i - c) for c in c_centers] for i in X])
# Get labels for each point
labels = deltas.argmin(1)
while True:
# Calculate mean of each cluster
new_c_centers = np.array([X[np.where(deltas.argmin(1) == i)[0]].mean(axis=0) for i in range(n_clusters)])
# Calculate distances again
deltas = np.array([[np.linalg.norm(i - c) for c in new_c_centers] for i in X])
# Get new labels for each point
labels = deltas.argmin(1)
# If there's no change in centers, exit
if np.array_equal(c_centers, new_c_centers):
break
c_centers = new_c_centers
return c_centers, labels
Grocery和Detergents_Paper将用于聚类,并且k将设置为3。 通常,应使用外观检查或弯头方法确定k,如下所示:
centers, labels = Kmeans_nD(df[['Grocery', 'Detergents_Paper']].values, 3)
现在,您可以使用以下命令在数据集中再添加一列:
df['labels'] = labels
您可以使用以下代码来首先可视化结果,以查看结果是否有意义:
## Creating data for the plotly
trace1 = go.Scatter(
# Extracting data based on label
x=df[df['labels'] == 0]['Grocery'],
y=df[df['labels'] == 0]['Detergents_Paper'],
mode='markers',
name='clust_1',
marker=dict(
size=12,
line=dict(
color='rgba(217, 217, 217, 0.14)',
width=0.5
),
opacity=0.8
)
)
trace2 = go.Scatter(
# Extracting data based on label
x=df[df['labels'] == 1]['Grocery'],
y=df[df['labels'] == 1]['Detergents_Paper'],
mode='markers',
name='clust_2',
marker=dict(
color='rgb(#3742fa)',
size=12,
symbol='circle',
line=dict(
color='rgb(204, 204, 204)',
width=1
),
opacity=0.9
)
)
trace3 = go.Scatter(
# Extracting data based on label
x=df[df['labels'] == 2]['Grocery'],
y=df[df['labels'] == 2]['Detergents_Paper'],
mode='markers',
name='clust_3',
marker=dict(
color='rgb(#ff4757)',
size=12,
symbol='circle',
line=dict(
color='rgb(104, 74, 114)',
width=1
),
opacity=0.9
)
)
data = [trace1, trace2, trace3]
### Layout settings
layout = go.Layout(
scene = dict(
xaxis = dict(
title= 'Grocery'),
yaxis = dict(title= 'Detergents_Paper'),
)
)
fig = go.Figure(data=data, layout=layout)
plot(fig)
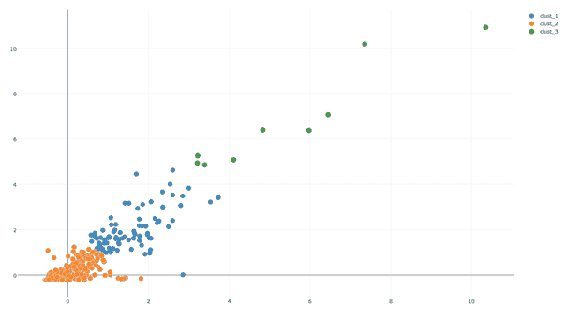
Plotting the clusters
乍一看,集群看起来很合理,并将最终取决于领域知识支持的解释。
您可以使用以下代码轻松查看每个集群每个特征的平均支出:
df.groupby('labels').mean()
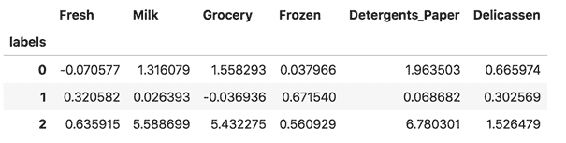
从这个简单的集群中可以看出,第三集群在Milk,Grocery和Detergents_Paper上的支出最高。 第二个集群的支出较低,第一个集群倾向于Milk,Grocery和Detergents_Paper,因此k=2也可以使用。
总结
在本章中,您学习了无监督学习的基础知识,并使用 K 均值算法进行聚类。
有许多聚类算法显示不同的行为。 当涉及到无监督学习算法时,可视化是关键,并且您已经看到了几种不同的方式来可视化和检查数据集。
在下一章中,您将学习 NumPy 常用的其他库,例如 SciPy,Pandas 和 scikit-learn。 这些都是从业者工具包中的重要库,它们相互补充。 您会发现自己将这些库与 NumPy 一起使用,因为每个库都会使某些任务变得更容易。 因此,重要的是要了解有关 Python 数据科学堆栈的更多信息。
六、NumPy,SciPy,Pandas 和 Scikit-Learn
到目前为止,您应该能够使用 NumPy 编写小型实现。 在整个章节中,我们旨在提供使用其他库的示例,在本章中,我们应退后一步,看看可以与 NumPy 一起用于项目的周围库。
本章将介绍其他 Python 库如何对 NumPy 进行补充。 我们将研究以下主题:
- NumPy 和 SciPy
- NumPy 和 Pandas
- SciPy 和 Scikit-learn
NumPy 和 SciPy
到目前为止,您已经看到了许多有关 NumPy 用法的示例,而只有少数 SciPy。 NumPy 具有数组数据类型,它允许您执行各种数组操作,例如排序和整形。
NumPy 具有一些数值算法,可用于执行诸如计算范数,特征值和特征向量之类的任务。 但是,如果数值算法是您的重点,则理想情况下应使用 SciPy,因为它包含更全面的算法集以及最新版本的算法。 SciPy 有许多有用的子程序包可用于某些类型的分析。
以下列表将使您对子软件包有一个整体的了解:
Cluster:此子程序包包含聚类算法。 它具有两个子模块vq和hierarchy。vq模块提供用于 K 均值聚类的函数。 层次结构模块包括用于层次结构聚类的函数。Fftpack:此子程序包包含用于快速傅立叶变换的函数和算法,以及差分和伪差分算符。Interpolate:此子程序包提供用于单变量和多变量插值的函数:1D 和 2D 样条曲线。Linalg:此子程序包提供用于线性代数的函数和算法,例如matrix运算和函数,特征值和-向量计算,矩阵分解,矩阵方程求解器和特殊矩阵。Ndimage:此子程序包提供用于多维图像处理的函数和算法,例如滤镜,插值,测量和形态。Optimize:此子程序包提供函数和算法,用于函数局部和全局优化,函数拟合,求根和线性编程。Signal:此子程序包提供信号处理的函数和算法,例如卷积,B 样条,滤波,连续和离散时间线性系统,波形,小波和频谱分析。Stats:此子程序包提供概率分布,例如连续分布,多元分布和离散分布,以及可以找到均值,众数,方差,偏度,峰度和相关系数的统计函数。
让我们来看一下其中的一个子包。 以下代码显示了用于群集分析的cluster程序包:
Scipy.cluster
%matplotlib inline
import matplotlib.pyplot as plt
### Import ndimage to read the image
from scipy import ndimage
### Import cluster for clustering algorithms
from scipy import cluster
### Read the image
image = ndimage.imread("cluster_test_image.jpg")
## Image is 1000x1000 pixels and it has 3 channels.
image.shape
(1000, 1000, 3)
这将为您提供以下输出:
array([[[30, 30, 30],
[16, 16, 16],
[14, 14, 14],
...,
[14, 14, 14],
[16, 16, 16],
[29, 29, 29]],
[[13, 13, 13],
[ 0, 0, 0],
[ 0, 0, 0],
...,
[ 0, 0, 0],
[ 0, 0, 0],
[12, 12, 12]],
[[16, 16, 16],
[ 3, 3, 3],
[ 1, 1, 1],
...,
[ 0, 0, 0],
[ 2, 2, 2],
[16, 16, 16]],
...,
[[17, 17, 17],
[ 3, 3, 3],
[ 1, 1, 1],
...,
[34, 26, 39],
[27, 21, 33],
[59, 55, 69]],
[[15, 15, 15],
[ 2, 2, 2],
[ 0, 0, 0],
...,
[37, 31, 43],
[34, 28, 42],
[60, 56, 71]],
[[33, 33, 33],
[20, 20, 20],
[17, 17, 17],
...,
[55, 49, 63],
[47, 43, 57],
[65, 61, 76]]], dtype=uint8)
在这里,您可以看到该图:
plt.figure(figsize = (15,8))
plt.imshow(image)
您可以从前面的代码块中获得以下图表:

使用以下代码将图像数组转换为二维数据集:
x, y, z = image.shape
image_2d = image.reshape(x*y, z).astype(float)
image_2d.shape
(1000000, 3)
image_2d
array([[30., 30., 30.],
[16., 16., 16.],
[14., 14., 14.],
...,
[55., 49., 63.],
[47., 43., 57.],
[65., 61., 76.]])
### kmeans will return cluster centers and the distortion
cluster_centers, distortion = cluster.vq.kmeans(image_2d, k_or_guess=2)
print(cluster_centers, distortion)
[[179.28653454 179.30176248 179.44142117]
[ 3.75308484 3.83491111 4.49236356]] 26.87835069294931
image_2d_labeled = image_2d.copy()
labels = []
from scipy.spatial.distance import euclidean
import numpy as np
for i in range(image_2d.shape[0]):
distances = [euclidean(image_2d[i], center) for center in cluster_centers]
labels.append(np.argmin(distances))
plt.figure(figsize = (15,8))
plt.imshow(cluster_centers[labels].reshape(x, y, z))
您从前面的代码中获得以下输出:
SciPy 和 NumPy 和线性回归
您已经了解了如何使用 NumPy 从头开始编写线性回归算法。Scipy.stats模块具有linregress函数,用于计算斜率,截距,相关系数(r 值),两侧 p 值以及标准差估计,如下所示:
from sklearn import datasets
%matplotlib inline
import matplotlib.pyplot as plt
### Boston House Prices dataset
boston = datasets.load_boston()
x = boston.data
y = boston.target
boston.feature_names
array(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT'], dtype='<U7')
x.shape
(506, 13)
y.shape
(506,)
### We will consider "lower status of population" as independent variable for its importance
lstat = x[0:,-1]
lstat.shape
(506,)
from scipy import stats
slope, intercept, r_value, p_value, std_err = stats.linregress(lstat, y)
print(slope, intercept, r_value, p_value, std_err)
-0.9500493537579909 34.55384087938311 -0.737662726174015 5.081103394387796e-88 0.03873341621263942
print("r-squared:", r_value**2)
r-squared: 0.5441462975864798
plt.plot(lstat, y, 'o', label='original data')
plt.plot(lstat, intercept + slope*lstat, 'r', label='fitted line')
plt.legend()
plt.show()
我们从前面代码的输出中获得以下图表,如下图所示:
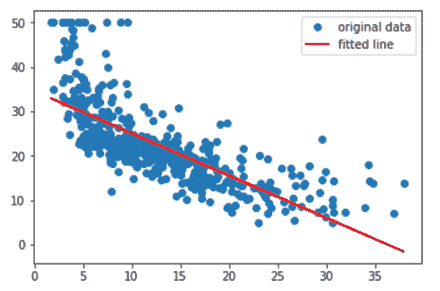
您还可以查看平均房间数与房价之间的关系。 以下代码块打印出性能指标:
rm = x[0:,5]
slope, intercept, r_value, p_value, std_err = stats.linregress(rm, y)
print(slope, intercept, r_value, p_value, std_err)
print("r-squared:", r_value**2)
### 9.102108981180308 -34.670620776438554 0.6953599470715394 2.48722887100781e-74 0.4190265601213402
## r-squared: 0.483525455991334
以下代码块绘制了拟合线:
plt.plot(rm, y, 'o', label='original data')
plt.plot(rm, intercept + slope*rm, 'r', label='fitted line')
plt.legend()
plt.show()
我们从前面的代码中获得以下输出,如下图所示:
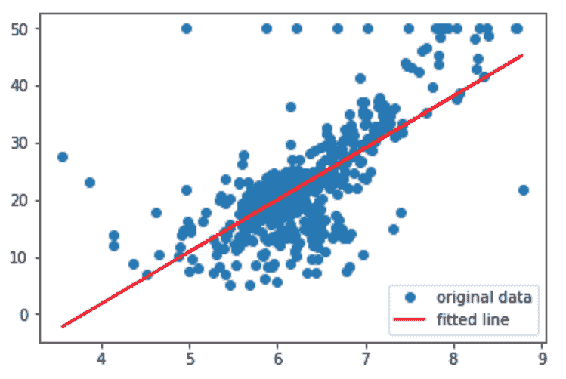
NumPy 和 Pandas
考虑一下时,NumPy 是一个相当低级的数组操作库,大多数其他 Python 库都写在它的顶部。
这些库之一是pandas,它是一个高级数据处理库。 浏览数据集时,通常会执行诸如计算描述性统计数据,按特定特征分组以及合并之类的操作。pandas库具有许多友好的函数来执行这些各种有用的操作。
在此示例中,我们使用糖尿病数据集。sklearn.datasets中的糖尿病数据集使用零均值和 L2 范数标准化。
该数据集包含 442 条记录,这些记录具有 10 个特征:年龄,性别,体重指数,平均血压和 6 个血清测量值。
目标代表采取这些基准措施后的疾病进展。 您可以在 web 和相关论文 中查看数据描述。
我们从操作开始,如下所示:
import pandas as pd
from sklearn import datasets
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
diabetes = datasets.load_diabetes()
df = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)
diabetes.feature_names
['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
df.head(10)
我们从前面的代码中获得以下输出,如下表所示:
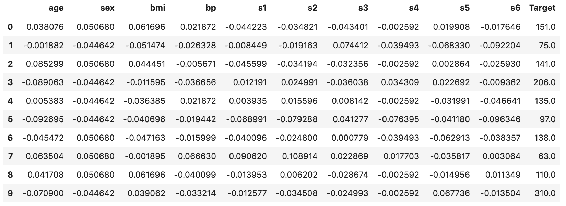
这段代码向您展示了如何在数据帧中创建目标列:
df['Target'] = diabetes.target
df.head(10)
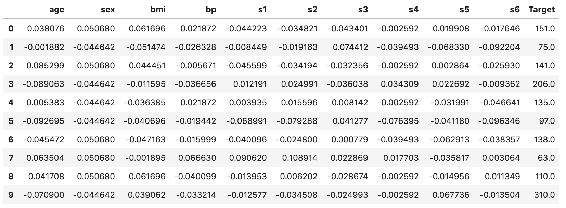
Pandas 帮助我们轻松地处理表格数据,并通过各种辅助方法和可视化支持我们的分析。 看一下代码:
## Descriptive statistics
df.describe()
我们从前面的代码中获得以下输出,如下表所示:

通过使用以下代码行,看看目标的分布方式:
plt.hist(df['Target'])
下图显示了上一行的输出:
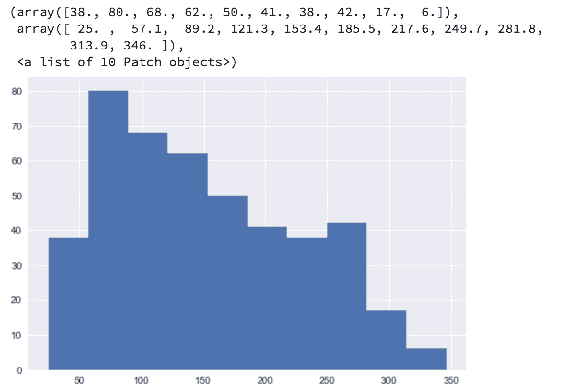
您可以看到目标变量向右倾斜。 看一下这段代码:
## Since 'sex' is categorical, excluding it from numerical columns
numeric_cols = [col for col in df.columns if col != 'sex']
numeric_cols
## ['age', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6', 'Target']
### You can have a look at variable distributions individually, but there's a better way
df[numeric_cols].hist(figsize=(20, 20), bins=30, xlabelsize=12, ylabelsize=12)
### You can also choose create dataframes for numerical and categorical variables
前一个代码块的输出:
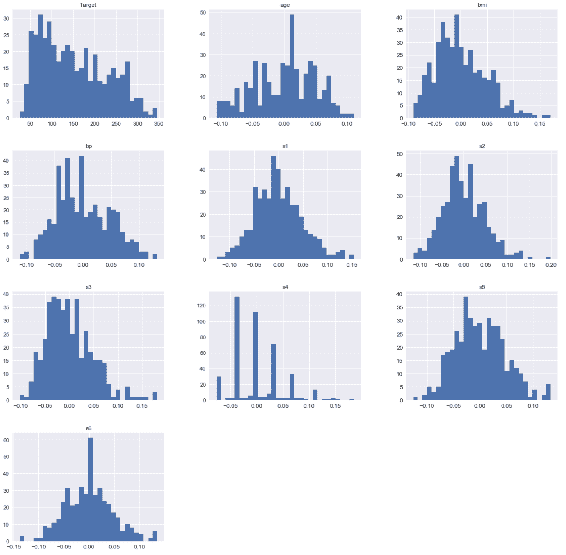
Feature distributions
您可以检查其中一些特征的分布,并确定其中哪些看起来相似。 对于此示例,特征s1,s2和s6似乎具有相似的分布,如从此代码中可以看到的:
## corr method will give you the correlation between features
df[numeric_cols].corr()
下图显示了上一行的输出:
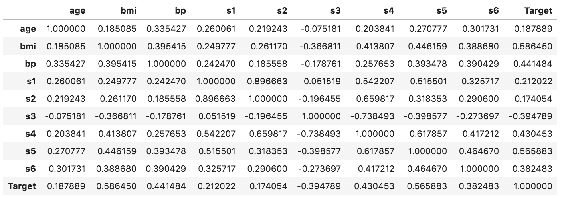
您可以使用heatmap更好地表示这种关系,如下所示:
plt.figure(figsize=(15, 15))
sns.heatmap(df[numeric_cols].corr(), annot=True)
下图是由前面的代码块生成的热图:
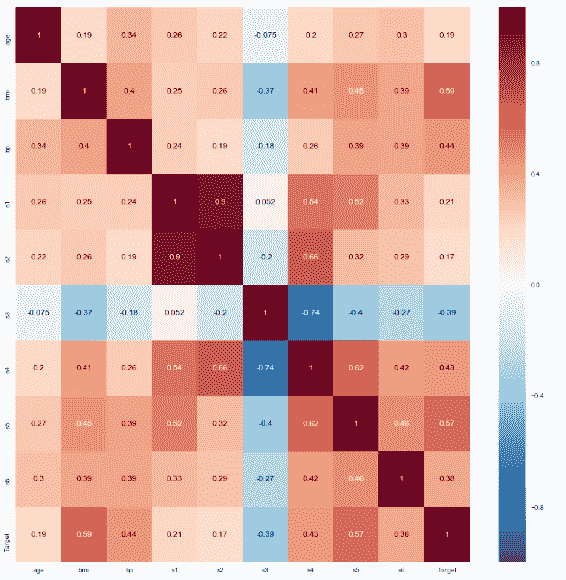
Correlations heatmap
您还可以通过以下方式过滤相关性:
plt.figure(figsize=(18, 15))
sns.heatmap(df[numeric_cols].corr()
[(df[numeric_cols].corr() >= 0.3) & (df[numeric_cols].corr() <= 0.5)],
annot=True)
此图显示了过滤后的相关性:
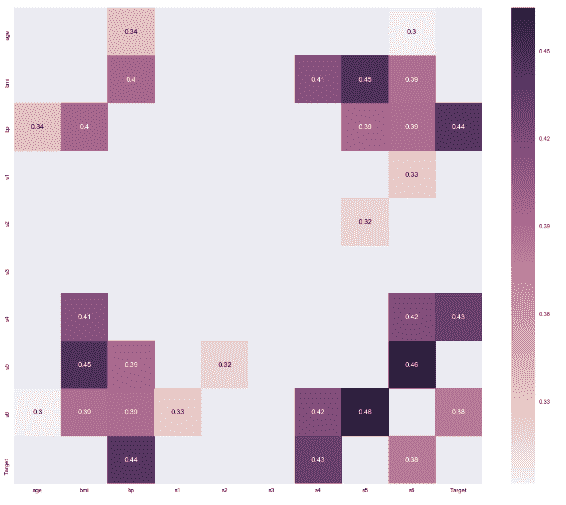
Filtered correlations heatmap
您还可以使用其他有用的可视化来检查统计关系,如下所示:
fig, ax = plt.subplots(3, 3, figsize = (18, 12))
for i, ax in enumerate(fig.axes):
if i < 9:
sns.regplot(x=df[numeric_cols[i]],y='Target', data=df, ax=ax)
该图显示了前面代码的以下输出:
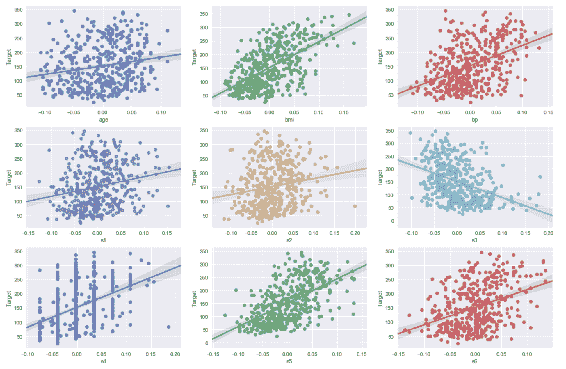
Regression Plots
您可以看到,使用pandas使探索性数据分析相对简单。 使用pandas,您可以检查特征及其关系。
Pandas 和股票价格的定量建模
pandas最初是为在金融数据集中使用而编写的,它包含许多用于处理时间序列数据的便捷函数。 在本节中,您将看到如何使用pandas库处理股票价格序列。
您将使用quandl Python 库获取公司的财务数据。 看一下这段代码:
import quandl msft = quandl.get('WIKI/MSFT')
msft.columns
## Index(['Open', 'High', 'Low', 'Close', 'Volume', 'Ex-Dividend', 'Split Ratio', 'Adj. Open', 'Adj. High', 'Adj. Low', 'Adj. Close', 'Adj. Volume'], dtype='object')
msft.tail()
下表显示了msft.tail()的输出:
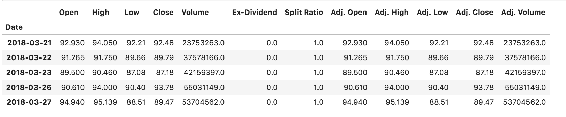
让我们通过导入以下设置来自定义绘图:
matplotlib.font_manager as font_manager font_path = '/Library/Fonts/Cochin.ttc' font_prop = font_manager.FontProperties(fname=font_path, size=24) axis_font = {'fontname':'Arial', 'size':'18'} title_font = {'fontname':'Arial', 'size':'22', 'color':'black', 'weight':'normal', 'verticalalignment':'bottom'} plt.figure(figsize=(10, 8)) plt.plot(msft['Adj. Close'], label='Adj. Close') plt.xticks(fontsize=22) plt.yticks(fontsize=22) plt.xlabel("Date", **axis_font) plt.ylabel("Adj. Close", **axis_font) plt.title("MSFT", **title_font) plt.legend(loc='upper left', prop=font_prop, numpoints=1) plt.show()
该图显示了来自先前设置的图:

您可以使用以下代码来计算每日变化:
msft['Daily Pct. Change'] = (msft['Adj. Close'] - msft['Adj. Open']) / msft['Adj. Open']
msft.tail(10)
下图显示了msft.tail(10)的输出:
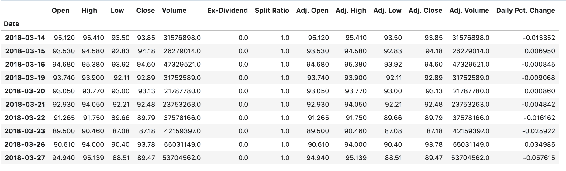
尝试使用此每日收益的直方图:
plt.figure(figsize=(22, 8))
plt.hist(msft['Daily Pct. Change'], bins=100)
如下图所示,它将为您提供以下图表:
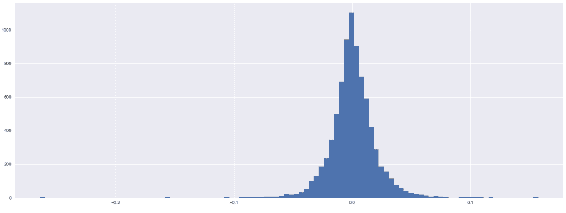
Distribution of daily returns
返回的分布具有较长的尾巴,尤其是在负侧,这是财务分析中的已知现象。 它产生的风险称为尾部风险,它与市场收益服从正态分布的假设相矛盾。 这基本上告诉您,极端事件发生的可能性比更正态分布的可能性更大。
在可视化方面,使它们具有交互性很有帮助。 为此,plotly提供了一个很好的替代当前绘图库的方法,如下所示:
import plotly.plotly as py
import plotly.graph_objs as go
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot init_notebook_mode(connected=True)
from datetime import datetime
import pandas_datareader.data as web
import quandl
msft = quandl.get('WIKI/MSFT')
msft['Daily Pct. Change'] = (msft['Adj. Close'] - msft['Adj. Open']) / msft['Adj. Open']
data = [go.Scatter(x=msft.index, y=msft['Adj. Close'])]
plot(data)
我们从前面的代码中获得以下图表,如下图所示:
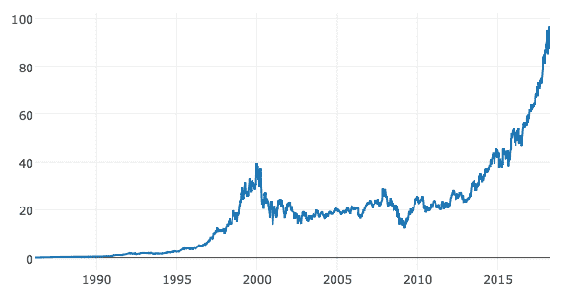
您可以创建开盘-最高-最低-收盘价(OHLC)的图表,其中每个日期都有 4 个不同的价格值,它们是开,高,低和关。 看一下这段代码:
charts trace = go.Ohlc(x=msft.index, open=msft['Adj. Open'], high=msft['Adj. High'], low=msft['Adj. Low'], close=msft['Adj. Close'])
data = [trace]
plot(data)
该图显示了先前代码的图:
您可以通过在图表上选择自定义范围来检查特定区域。 看一下这个图:
同样,您可以使用以下代码创建Candlestick图表:
trace = go.Candlestick(x=msft.index, open=msft['Adj. Open'], high=msft['Adj. High'], low=msft['Adj. Low'], close=msft['Adj. Close'])
data = [trace]
plot(data)
下图显示了此代码的输出:
您也可以在Candlestick图表中选择特定范围。 看一下这个图:
分布图如下:
import plotly.figure_factory as ff
fig = ff.create_distplot([msft['Daily Pct. Change'].values], ['MSFT Daily Returns'], show_hist=False)
plot(fig)
下图显示了前面代码的输出:
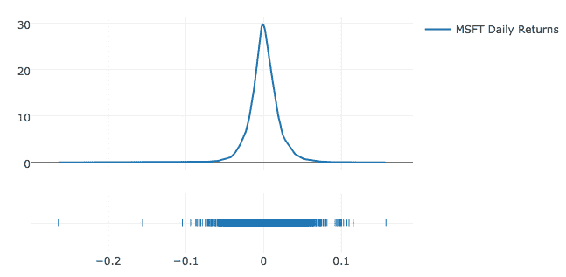
我们可以创建三个移动平均线,如下所示:
msft['200MA'] = msft['Adj. Close'].rolling(window=200).mean()
msft['100MA'] = msft['Adj. Close'].rolling(window=100).mean()
msft['50MA'] = msft['Adj. Close'].rolling(window=50).mean()
msft.tail(10)
下表显示了msft.tail(10)的输出:
根据切片的数据,将包括最近 2,000 天。 看一下这段代码:
trace_adjclose = go.Scatter( x=msft[-2000:].index, y=msft[-2000:]['Adj. Close'], name = "Adj. Close", line = dict(color = '#000000'), opacity = 0.8)
trace_200 = go.Scatter( x=msft[-2000:].index, y=msft[-2000:]['200MA'], name = "200MA", line = dict(color = '#FF0000'), opacity = 0.8)
trace_100 = go.Scatter( x=msft[-2000:].index, y=msft[-2000:]['100MA'], name = "100MA", line = dict(color = '#0000FF'), opacity = 0.8)
trace_50 = go.Scatter( x=msft[-2000:].index, y=msft[-2000:]['50MA'], name = "50MA", line = dict(color = '#FF00FF'), opacity = 0.8)
data = [trace_adjclose, trace_200, trace_100, trace_50]
layout = dict( title = "MSFT Moving Averages: 200, 100, 50 days", )
fig = dict(data=data, layout=layout)
plot(fig)
下图显示了前面代码块中的图:
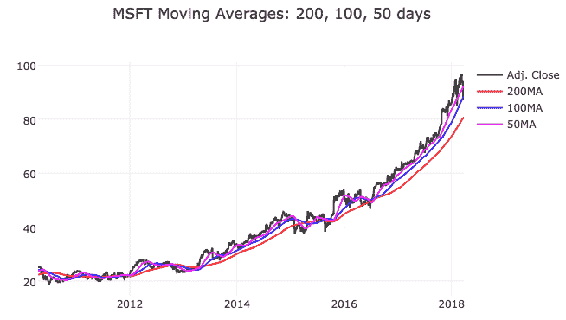
移动平均线用于监视金融市场的趋势。 在此示例中,有三个移动平均线,每个移动线均具有不同的周期。 您可以设置分析天数,以进行短期,中期和长期趋势监视。
当您开始使用财务时间序列时,您会很快意识到您需要基于不同期间的汇总,并且在pandas中创建这些汇总非常容易。 以下代码段将通过计算平均值每月汇总记录:
msft_monthly = msft.resample('M').mean()
msft_monthly.tail(10)
下图显示了msft_monthly.tail(10)的输出:
这是一个简单的时间序列图:
data = [go.Scatter(x=msft_monthly[-24:].index, y = msft_monthly[-24:]['Adj. Close'])]
plot(data)
如下图所示,这将为您提供以下图表:
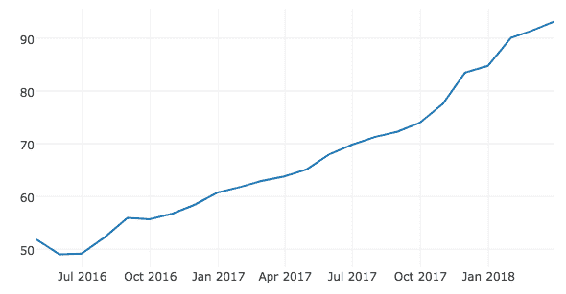
在检查要素之间的关系时,可以使用我们在前面的示例中已经看到的相关矩阵。 在时间序列中,从业者对自相关感兴趣,自相关显示了时间序列与其自身的相关性。 例如,理想情况下,您希望时间序列中出现周期性的峰值,以显示您的季节性。 通过使用以下代码,让我们看看每日百分比变化是否有任何明显的峰值:
plt.figure(figsize=(22, 14)) pd.plotting.autocorrelation_plot(msft_monthly['Daily Pct. Change'])
我们从前面的代码中获得以下图表,如下图所示:
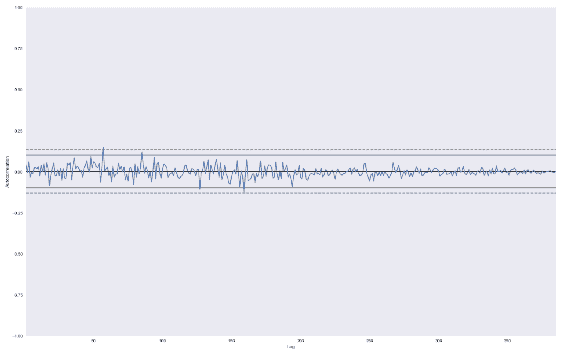
Monthly autocorrelation plot
在这个系列中没有有意义的显着滞后,但是如果您使用宏观经济变量(例如 GDP,通货膨胀率和失业水平)进行尝试,则可能会看到显着的季度或年度峰值。
SciPy 和 Scikit-learn
Scikit-learn 是用于机器学习的 SciKit 库之一,它建立在 SciPy 之上。 您可以使用它执行回归分析,就像在前几章中使用 scikit-learn 库所做的那样。 看一下这段代码:
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
diabetes = datasets.load_diabetes()
linreg = linear_model.LinearRegression()
linreg.fit(diabetes.data, diabetes.target)
### You can inspect the results by looking at evaluation metrics
print('Coeff.: n', linreg.coef_)
print("MSE: {}".format(mean_squared_error(diabetes.target, linreg.predict(diabetes.data)))) print('Variance Score: {}'.format(r2_score(diabetes.target, linreg.predict(diabetes.data))))
scikit-learn 和住房数据的 K 均值聚类
在本节中,我们将使用 scikit-learn 的 K 均值算法对房屋数据进行聚类,如下所示:
from sklearn.cluster import KMeans from sklearn.datasets import load_boston boston = load_boston()
## As previously, you have implemented the KMeans from scracth and in this example, you use sklearns API k_means = KMeans(n_clusters=3) # Training k_means.fit(boston.data)
KMeans(algorithm='auto', copy_x=True, init='K 均值++', max_iter=300, n_clusters=3, n_init=10, n_jobs=1, precompute_distances='auto', random_state=None, tol=0.0001, verbose=0)
print(k_means.labels_)
前面代码的输出如下:
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 0 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 0 0 0 0 0 0 0 0 0 0 0 2 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 2 2
2 0 2 2 2 2 0 2 2 2 0 0 0 0 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1]
您可以使用以下代码行检查群集中心:
print(k_means.cluster_centers_)
这是控制台的输出:
[[ 1.49558803e+01 -5.32907052e-15 1.79268421e+01 2.63157895e-02
6.73710526e-01 6.06550000e+00 8.99052632e+01 1.99442895e+00
2.25000000e+01 6.44736842e+02 1.99289474e+01 5.77863158e+01
2.04486842e+01]
[ 3.74992678e-01 1.57103825e+01 8.35953552e+00 7.10382514e-02
5.09862568e-01 6.39165301e+00 6.04133880e+01 4.46074481e+00
4.45081967e+00 3.11232240e+02 1.78177596e+01 3.83489809e+02
1.03886612e+01]
[ 1.09105113e+01 5.32907052e-15 1.85725490e+01 7.84313725e-02
6.71225490e-01 5.98226471e+00 8.99137255e+01 2.07716373e+00
2.30196078e+01 6.68205882e+02 2.01950980e+01 3.71803039e+02
1.78740196e+01]]
关于聚类算法的评估,通常将使用诸如轮廓分析或弯头方法之类的技术来评估聚类的质量并确定正确的超参数(例如 K 均值)。 使用 scikit-learn 提供的简单 API,您还将发现这种分析易于执行。 强烈建议您通过实践从这些示例中学到的知识为基础,这将提高您的知识和技能。
总结
在本章中,您使用各种示例(主要用于机器学习任务)练习了 NumPy,SciPy,Pandas 和 scikit-learn。 使用 Python 数据科学库时,通常有不止一种执行给定任务的方法,而且通常有助于了解不止一种方法。
您可以使用替代方法以获得更好的实现,也可以出于比较的目的。 在为给定任务尝试不同的方法时,您可能会找到不同的选项,这些选项将允许您进一步自定义实现,或者只是观察到一些性能改进。
本章的目的是向您展示这些不同的选项,以及 Python 语言由于其丰富的分析库生态系统而具有的灵活性。 在下一章中,您将了解有关 NumPy 内部的更多信息,例如 numpy 如何管理数据结构和内存,代码概要分析以及有效编程的技巧。
七、高级 NumPy
许多库都具有易于使用的 API。 您需要做的就是调用提供的 API 函数,库将为您处理其余的函数。 幕后发生的事情与您无关,您只对输出感兴趣。 在大多数情况下,这很好,但是,至少要了解所使用库的基本内部结构很重要。 了解内部结构将帮助您掌握代码的最新动态以及开发应用时应避免的危险信号。
在本章中,将回顾 NumPy 的内部结构,例如 NumPy 的类型层次结构和内存使用情况。 在本章的最后,您将了解用于逐行检查程序的代码配置文件。
NumPy 内部
如您在前几章中所见,NumPy 数组使数值计算变得高效,其 API 直观且易于使用。 NumPy 数组也是其他科学图书馆的核心,因为其中许多库都是基于 NumPy 数组构建的。
为了编写更好,更高效的代码,您需要了解数据处理的内部。 NumPy 数组及其元数据位于数据缓冲区中,该缓冲区是带有某些数据项的专用内存块。
NumPy 如何管理内存?
初始化 NumPy 数组后,其元数据和数据将存储在随机存取存储器(RAM)中分配的存储位置上。
import numpy as np
array_x = np.array([100.12, 120.23, 130.91])
首先,Python 是一种动态类型化的语言; 不需要显式声明变量类型,例如int或double。 可以推断变量类型,在这种情况下,您希望array_x的数据类型为np.float64:
print(array_x.dtype)
float64
使用numpy库而不是 Python 的优势在于numpy支持许多不同的数值数据类型,例如bool_,int_,intc,intp,int8,int16,int32,int64,uint8,uint16,uint32,uint64,float_,float16,float32,float64,complex_,complex64和complex128。
您可以通过检查sctypes查看这些类型:
np.sctypes
{'complex': [numpy.complex64, numpy.complex128, numpy.complex256],
'float': [numpy.float16, numpy.float32, numpy.float64, numpy.float128],
'int': [numpy.int8, numpy.int16, numpy.int32, numpy.int64],
'others': [bool, object, bytes, str, numpy.void],
'uint': [numpy.uint8, numpy.uint16, numpy.uint32, numpy.uint64]}
下图显示了数据类型树:
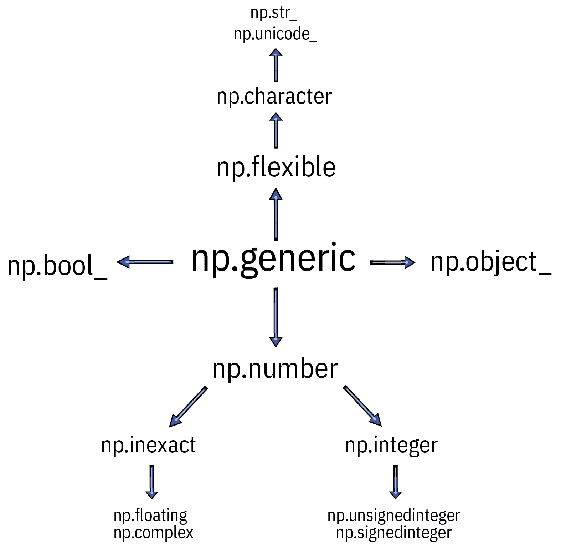
您可以通过调用mro方法来检查诸如np.float64之类的数据类型的父类:
np.float64.mro()
[numpy.float64,
numpy.floating,
numpy.inexact,
numpy.number,
numpy.generic,
float,
object]
和np.int64的父类:
np.int64.mro()
[numpy.int64,
numpy.signedinteger,
numpy.integer,
numpy.number,
numpy.generic,
object]
mro方法代表“方法解析顺序”。 为了更好地理解继承,应该首先了解继承的概念。 在可以使用面向对象范例的编程语言中,可以将对象的属性和方法基于之前创建的另一个对象,这就是继承。 在前面的示例中,np.int64保留了np.signedinteger及其之后的属性和行为。
让我们看一个简单的例子:
class First:
def firstmethod(self):
print("Call from First Class, first method.")
class Second:
def secondmethod(self):
print("Call from Second Class, second method.")
class Third(First, Second):
def thirdmethod(self):
print("Call from Third Class, third method.")
这里,有 3 个类别,而First和Second类别是独立的,Third类别是从First和Second继承的。 您可以创建Third类的实例,并使用dir方法检查其内容:
myclass = Third()
dir(myclass)
[...
'__repr__',
'__setattr__',
'__sizeof__',
'__str__',
'__subclasshook__',
'__weakref__',
'firstmethod',
'secondmethod',
'thirdmethod']
dir表示myclass的方法中有firstmethod,secondmethod和thirdmethod。
您可以调用这些方法,如下所示:
myclass.firstmethod()
myclass.secondmethod()
myclass.thirdmethod()
## Call from First Class, first method.
## Call from Second Class, second method.
## Call from Third Class, third method.
现在,让我们向Second类添加firstmethod,看看会发生什么:
class First:
def firstmethod(self):
print("Call from First Class, first method.")
class Second:
def firstmethod(self):
print("Call from Second Class, first method.")
def secondmethod(self):
print("Call from Second Class, second method.")
class Third(First, Second):
def thirdmethod(self):
print("Call from Third Class, third method.")
像以前一样检查方法输出:
myclass = Third()
myclass.firstmethod()
myclass.secondmethod()
myclass.thirdmethod()
## Call from First Class, first method.
## Call from Second Class, second method.
## Call from Third Class, third method.
如您所见,已添加到Second类的方法无效,因为Third类的实例从First类继承了该实例。
您可以按以下方式检查类的mro:
Third.__mro__
这将为您提供以下输出:
(__main__.Third, __main__.First, __main__.Second, object)
这是使用继承机制时解析属性和方法的方式,并且现在您应该或多或少地了解mro的工作方式。 现在,您可以再次查看我们之前拥有的 numpy 数据类型的mro示例。
您可以使用nbytes来查看存储数据类型所需的内存。
首先,让我们看看单个float64的大小:
np.float64(100.12).nbytes
8
np.str_('n').nbytes
4
np.str_('numpy').nbytes
20
array_x具有 3 个float64,其大小将是元素数乘以商品大小,即24,如以下代码段所示:
np.float64(array_x).nbytes
24
例如,如果您需要较低的计算精度,则可以使用np.float32,它将占用float64占用的一半内存:
array_x2 = array_x.astype(np.float32)
array_x2
array([100.12, 120.23, 130.91], dtype=float32)
np.float32(array_x2).nbytes
12
简单来说,8 个字节的内存将保存 1 float64或 2 float32。
Python 的动态性质引入了一种处理数据类型的新方法,因为 Python 应该包含有关其存储的数据的更多信息。 虽然典型的 C 变量将具有有关内存位置的信息,但 Python 变量应具有存储为 C 结构的信息,该结构包含引用计数,对象的类型,对象的大小以及变量本身。
这是提供灵活的环境来处理不同数据类型所必需的。 如果诸如列表之类的数据结构可以容纳不同类型的对象,这是由于该信息对于列表中的每个元素的存储。
但是,由于 NumPy 数组中的数据类型是固定的,由于使用了连续的内存块,因此内存使用效率可能更高。
您可以通过检查 NumPy 数组的__array_interface__属性来查看地址和其他相关信息。
编写此接口是为了允许开发人员共享数组内存和信息:
array_x.__array_interface__
{'data': (140378873611440, False),
'descr': [('', '<f8')],
'shape': (3,),
'strides': None,
'typestr': '<f8',
'version': 3}
__array_interface__是具有 6 个键的 python 字典:
shape的工作方式类似于 NumPy 数组或pandas数据帧的常规shape属性。 它显示每个大小的大小。 由于array_x具有1大小和3元素,因此它是具有3大小的元组。typestr具有3值,第一个显示字节顺序,第二个显示字符代码,其余字符显示字节数。 在此示例中,其值为`’,这表示字节顺序为低位字节序,字符代码为浮点,并且使用的字节数为 8。descr可能会提供有关内存布局的更多详细信息。 默认值为[('', typestr)]。data显示数据的存储位置。 这是一个元组,其中第一个元素显示 NumPy 数组的存储块地址,第二个元素是指示其是否为只读的标志。 在此示例中,内存块地址为140378873611440,它不是只读的。strides指示给定的数组是否为 C 样式的连续内存缓冲区。 在此示例中,None 表示这是 C 样式的连续数组。 否则,它将包含跨步元组,以了解跳转到给定维度中的下一个数组元素所要跳转的位置。 步幅是重要的属性,因为当您使用不同的切片(例如X[::4])时,步幅将引导数组视图。version表示在此示例中版本号为 3。
以下片段显示了一个简单的示例:
import numpy as np
X = np.array([1,2,3,2,1,3,9,8,11,12,10,11,14,25,26,24,30,22,24,27])
X[::4]
## array([ 1, 1, 11, 14, 30])
这一点很重要,因为当您使用基于现有ndarrays的切片创建新的ndarrays时,可能会降低性能。 让我们看一个简单的例子; 以下代码段创建了 3D ndarray:
nd_1 = np.random.randn(4, 6, 8)
nd_1
## array([[[ 0.64900179, -0.00494884, -0.97565618, -0.78851039],
[ 0.05165607, 0.068948 , 1.54542042, 1.68553396],
[-0.80311258, 0.95298682, -0.85879725, 0.67537715]],
[[ 0.24014811, -0.41894241, -0.00855571, 0.43483418],
[ 0.43001636, -0.75432657, 1.16955535, -0.42471807],
[ 0.6781286 , -1.87876591, 1.02969921, 0.43215107]]])
您可以对其进行切片并创建另一个数组:
nd_2 = nd_1[::, ::2, ::2]
将会选择:
- 首先,第一维的所有项目
- 然后,第二维的每两个项目
- 然后,第三维的每两个项目
它将具有以下数组:
print(nd_2)
[[[ 0.64900179 -0.97565618]
[-0.80311258 -0.85879725]]
[[ 0.24014811 -0.00855571]
[ 0.6781286 1.02969921]]]
您可以看到nd_1和nd_2的内存地址相同:
nd_1.__array_interface__
{'data': (140547049888960, False),
'descr': [('', '<f8')],
'shape': (2, 3, 4),
'strides': None,
'typestr': '<f8',
'version': 3}
nd_2.__array_interface__
{'data': (140547049888960, False),
'descr': [('', '<f8')],
'shape': (2, 2, 2),
'strides': (96, 64, 16),
'typestr': '<f8',
'version': 3}
nd_2大步前进,了解如何沿nd_1数组的不同维度移动。
为了强调这些跨步在数值计算中的作用,下面的示例将为数组维和切片使用更大的大小:
nd_1 = np.random.randn(400, 600)
nd_2 = np.random.randn(400, 600*20)[::, ::20]
nd_1和nd_2具有相同的大小:
print(nd_1.shape, nd_2.shape)
(400, 600) (400, 600)
您可以测量用于计算nd_1和nd_2的数组元素的累积乘积的时间:
%%timeit
np.cumprod(nd_1)
## 802 µs ± 20.2 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
%%timeit
np.cumprod(nd_2)
## 12 ms ± 71.7 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
两次操作之间存在明显的时间差; 这是为什么? 如您所料,nd_2中的步幅过大会导致此问题:
nd_1.__array_interface__
{'data': (4569473024, False),
'descr': [('', '<f8')],
'shape': (400, 600),
'strides': None,
'typestr': '<f8',
'version': 3}
nd_2.__array_interface__
{'data': (4603252736, False),
'descr': [('', '<f8')],
'shape': (400, 600),
'strides': (96000, 160),
'typestr': '<f8',
'version': 3}
从存储器向 CPU 读取数据时,nd_2中存在跨步会导致跳转到不同的存储器位置。 如果将数组元素顺序存储为连续的内存块,那么从时间测量来看,此操作会更快。 步伐越小越好,可以更好地利用 CPU 缓存来提高性能。
有一些变通办法可以缓解与 CPU 缓存相关的问题。 您可以使用的一种库是numexpr库,它是 NumPy 的快速数值表达式求值器。 库使内存使用效率更高,并且还可以使多线程编程受益,以充分利用可用的内核。 您也可以将其与 Intel 的 VML 结合使用以进行进一步的改进。
在下面的示例中,让我们看看它是否对nd_2有帮助:
import numexpr as ne
%%timeit
2 * nd_2 + 48
## 4 ms ± 10.9 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
%%timeit
ne.evaluate("2 * nd_2 + 48")
## 843 µs ± 8.1 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
您应该使用其他示例进行尝试,以查看性能提升。
如果从头开始索引数组到某个元素,您将看到它具有相同的内存地址:
array_x[:2].__array_interface__['data'][0]
## 140378873611440
array_x[:2].__array_interface__['data'][0] == array_x.__array_interface__['data'][0]
## True
但是,如果您在0以外的位置开始索引,则将为您提供不同的内存地址:
array_x[1:].__array_interface__['data'][0]
## 140378873611448
array_x[1:].__array_interface__['data'][0] == array_x.__array_interface__['data'][0]
## False
ndarray的另一个属性称为标志,它提供有关给定 NumPy 数组的内存布局的信息:
array_f = np.array([[100.12, 120.23, 130.91], [90.45, 110.32, 120.32]])
print(array_f)
## [[100.12 120.23 130.91]
## [ 90.45 110.32 120.32]]
array_f.flags
## C_CONTIGUOUS : True
## F_CONTIGUOUS : False
## OWNDATA : True
## WRITEABLE : True
## ALIGNED : True
## WRITEBACKIFCOPY : False
## UPDATEIFCOPY : False
您可以使用类似于字典的符号或小写的属性名称来获得单个标志:
array_f.flags['C_CONTIGUOUS']
## True
array_f.flags.c_contiguous
## True
让我们看一下每个属性:
C_CONTIGUOUS:C 样式的连续内存的单个块F_CONTIGUOUS:连续内存的单个块,Fortran 风格
您的数据可以使用不同的布局存储在内存中。 这里有 2 种不同的内存布局要考虑:对应于C_CONTIGUOUS的行主要顺序和对应于F_CONTIGUOUS的列主要顺序。
在该示例中,array_f是二维的,array_f的行项目存储在相邻的存储位置中。 类似地,在F_CONTIGUOUS情况下,每列的值存储在相邻的存储位置中。
某些numpy函数将使用参数order将此顺序指示为'C'或'F'。 以下示例显示了具有不同顺序的reshape函数:
np.reshape(array_f, (3, 2), order='C')
## array([[100.12, 120.23],
## [130.91, 90.45],
## [110.32, 120.32]])
np.reshape(array_f, (3, 2), order='F')
## array([[100.12, 110.32],
## [ 90.45, 130.91],
## [120.23, 120.32]])
其余的:
OWNDATA:数组是否与另一个对象共享其内存块或拥有所有权WRITEABLE:False表示它是只读的; 否则可以将该区域写入。ALIGNED:数据是否针对硬件对齐WRITEBACKIFCOPY:该数组是否是另一个数组的副本UPDATEIFCOPY:(不建议使用WRITEBACKIFCOPY)
了解内存管理很重要,因为它会影响性能。 根据您执行计算的方式,计算速度会有所不同。 您可能没有意识到某些计算涉及现有数组的隐式副本,这会减慢计算速度。
以下代码块显示了两个示例,其中第一个不需要复制,而第二个具有隐式复制操作:
shape = (400,400,400)
array_x = np.random.random_sample(shape)
import cProfile
import re
cProfile.run('array_x *= 2')
### 3 function calls in 0.065 seconds
## Ordered by: standard name
## ncalls tottime percall cumtime percall filename:lineno(function)
## 1 0.065 0.065 0.065 0.065 <string>:1(<module>)
## 1 0.000 0.000 0.065 0.065 {built-in method builtins.exec}
## 1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}
import cProfile
import re
cProfile.run('array_y = array_x * 2')
### 3 function calls in 0.318 seconds
## Ordered by: standard name
## ncalls tottime percall cumtime percall filename:lineno(function)
## 1 0.318 0.318 0.318 0.318 <string>:1(<module>)
## 1 0.000 0.000 0.318 0.318 {built-in method builtins.exec}
## 1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}
首次运行比第二次慢 5 倍。 您需要了解隐式复制操作,并熟悉它在哪种情况下发生。 重塑数组不需要隐式复制,除非它是矩阵转置。
许多数组操作会返回一个新数组以获取结果。 此行为是预期的,但会破坏迭代任务的性能,在迭代任务中,您可能会有数百万或数十亿次迭代。 某些numpy函数具有out参数,该参数创建输出数组,并使用其写入迭代结果。 通过这种方式,您的程序可以更好地管理内存,并且需要更少的时间:
shape_x = (8000,3000)
array_x = np.random.random_sample(shape_x)
%%timeit
np.cumprod(array_x)
## 176 ms ± 2.32 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
output_array的类型和大小应与操作的预期输出相同:
output_array = np.zeros(array_x.shape[0] * array_x.shape[1])
%%timeit
np.cumprod(array_x, out=output_array)
## 86.4 ms ± 1.21 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
对 NumPy 代码进行性能分析以了解性能
有几个有用的库可以监视给定 python 脚本的性能指标。 您已经看到cProfile库的用法。 本节将介绍vprof,它是可视分析器库。
它将为您提供给定 python 程序的运行时统计信息和内存利用率。
第 5 章“使用 NumPy 聚类批发分销商的客户”的一维特征将在此处使用,以下代码段应保存到名为to_be_profiled.py的文件中:
import numpy as np
X = np.array([1,2,3,2,1,3,9,8,11,12,10,11,14,25,26,24,30,22,24,27])
n_clusters = 3
def Kmeans_1D(X, n_clusters, random_seed=442):
# Randomly choose random indexes as cluster centers
rng = np.random.RandomState(random_seed)
i = rng.permutation(X.shape[0])[:n_clusters]
c_centers = X[i]
# Calculate distances between each point and cluster centers
deltas = np.array([np.abs(point - c_centers) for point in X])
# Get labels for each point
labels = deltas.argmin(1)
while True:
# Calculate mean of each cluster
new_c_centers = np.array([X[np.where(deltas.argmin(1) == i)[0]].mean() for i in range(n_clusters)])
# Calculate distances again
deltas = np.array([np.abs(point - new_c_centers) for point in X])
# Get new labels for each point
labels = deltas.argmin(1)
# If there's no change in centers, exit
if np.all(c_centers == new_c_centers):
break
c_centers = new_c_centers
return c_centers, labels
c_centers, labels = Kmeans_1D(X, 3)
print(c_centers, labels)
保存此文件后,您可以使用命令行开始对其进行性能分析。
可以通过 4 种不同的方式配置vprof来获取:
- CPU 火焰图(
vprof -c c to_be_profiled.py) - 内置的探查器统计信息(
vprof -c p to_be_profiled.py) - 运行程序中的行后,Cpython 垃圾收集器跟踪的对象和进程内存的内存图(
vprof -c m to_be_profiled.py) - 用
runtime编码heatmap并为每条执行的行计数(vprof -c h to_be_profiled.py)
这 4 种配置可用于单个源文件或包。 让我们看一下p,m和h配置的输出:
探查器的配置:
$ vprof -c p to_be_profiled.py
Running Profiler...
[10.71428571 25.42857143 2\. ] [2 2 2 2 2 2 0 0 0 0 0 0 0 1 1 1 1 1 1 1]
Starting HTTP server...
一个新的选项卡将在您的浏览器中打开,并显示以下输出:
Time spent for each call
您可以看到文件名,函数名,行号和每次调用所花费的时间。
内存使用情况统计信息的配置:
$ vprof -c m to_be_profiled.py
Running MemoryProfiler...
[10.71428571 25.42857143 2\. ] [2 2 2 2 2 2 0 0 0 0 0 0 0 1 1 1 1 1 1 1]
Starting HTTP server...
新标签页将在您的浏览器中打开,并显示以下输出:
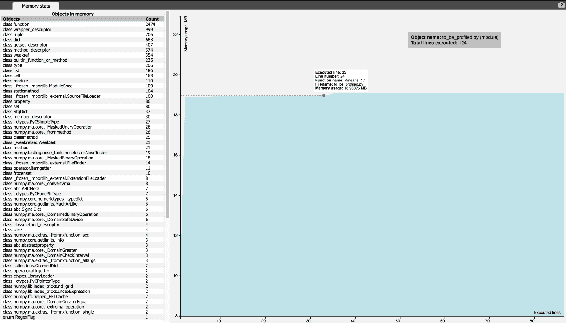
内存使用情况
在左侧,您可以看到内存中的对象,并且图表显示了随着执行的行数增加,内存使用量(以兆字节为单位)。 如果将鼠标悬停在图表上,则每个点将具有以下信息:
- 执行的行
- 行号
- 函数名称
- 文件名称
- 内存使用情况
例如,to_be_profiled.py文件中的第 27 行是计算deltas的下一行:
deltas = np.array([np.abs(point - new_c_centers) for point in X])
它执行了很多次,因为如果您检查图表,这是列表理解。
代码heatmap的配置:
$ vprof -c h to_be_profiled.py
Running CodeHeatmapProfiler...
[10.71428571 25.42857143 2\. ] [2 2 2 2 2 2 0 0 0 0 0 0 0 1 1 1 1 1 1 1]
Starting HTTP server...
“新”标签将在您的浏览器中打开,并显示以下输出:
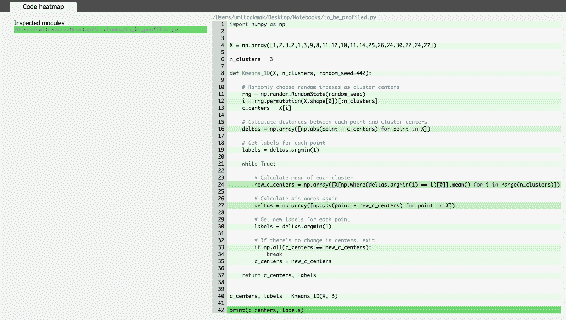
Heatmap for the lines executed
在左侧,有一个已检查模块的列表,在这种情况下,只有一个文件要检查。
右边是程序中每行的热图。 如果将鼠标悬停在行上,它将为您提供以下信息:
- 花费的时间
- 总运行时间
- 百分比
- 运行计数
如果将鼠标悬停在27行上,它将为您提供以下统计信息:

总结
在进行科学操作时,了解 NumPy 的内部结构至关重要。 效率是关键,因为许多科学计算都是计算和内存密集型的。 因此,如果您的代码编写效率不高,则计算所需的时间将远远超过所需的时间,这将损害您的研发时间。
在本章中,您已经了解了 NumPy 库的一些内部和性能方面,还了解了vprof库,该库可帮助您检查 python 程序的性能。
代码概要分析将极大地帮助您逐行检查程序,并且如您先前所见,查看相同数据的方式也有所不同。 确定了程序中最苛刻的部分后,便可以开始搜索更有效的方法或实现以提高性能并节省更多时间。
在下一章中,我们将概述高性能,低级的数值计算库。 NumPy 可以使用这些实现来获得可观的性能提升。
八、高性能数值计算库概述
在科学计算应用中可以执行许多数值运算,并且未经优化的代码或库实现会导致严重的性能瓶颈。
NumPy 库通过更有效地使用其内存布局来帮助提高 Python 程序的性能。
在实际应用中,最常用的数学分支之一是线性代数。 线性代数用于计算机图形学,密码学,计量经济学,机器学习,深度学习和自然语言处理,仅举几个例子。 具有高效的矩阵和向量运算至关重要。
高性能,低级框架(例如 BLAS,LAPACK 和 ATLAS)是 Netlib 库的一部分,用于密集的线性代数运算;其他框架(例如 Intel MKL)也可以在其中使用您的程序。 这些库在计算中具有很高的性能和准确性。 您可以通过其他高级编程语言(例如 Python 或 C++)调用它们来使用这些库。
当 NumPy 与不同的 BLAS 库链接时,您可以观察到性能差异而无需更改代码,因此了解哪种链接可以更好地提高性能非常重要。
让我们看一下这些低级库。
BLAS 和 LAPACK
BLAS 代表基本线性代数子程序,并且是处理线性代数运算的低级例程的标准。 低级例程包括向量和矩阵加/乘,线性组合等操作。 BLAS 为线性代数运算提供了三种不同的级别:
- BLAS1:标量向量和向量向量运算
- BLAS2:矩阵向量运算
- BLAS3:矩阵矩阵运算
LAPACK 代表线性代数软件包,并包含更高级的操作。 LAPACK 提供了用于矩阵分解(例如 LU,Cholesky 和 QR)以及解决特征值问题的例程。 LAPACK 主要取决于 BLAS 例程。
ATLAS
有许多优化的 BLAS 实现。 ATLAS 代表自动调谐线性代数软件,并且是与平台无关的项目,可以生成优化的 BLAS 实现。
英特尔 MKL
英特尔 MKL 为英特尔处理器优化了 BLAS。 改进了例程和函数,例如 1 级,2 级和 3 级 BLAS,LAPACK 例程,求解器,FFT 函数,其他数学和统计函数。 这些改进的例程和函数得益于共享内存多处理等改进,它们可用于在发行版(如 Anaconda 发行版)中加速科学 python 库(例如 NumPy 和 SciPy)。 如果您查看其发行说明, 可以看到每个发行版都进行了一些重要的改进,例如 LAPACK 函数的性能得到了提高。
OpenBLAS
OpenBLAS 是另一个优化的 BLAS 库,它为不同的配置提供了 BLAS3 级的优化。 作者报告说,与 BLAS 相比,性能增强和改进可与英特尔 MKL 的性能相媲美。
使用 AWS EC2 和底层库配置 NumPy
- 登录到 AWS。 如果您没有帐户,请创建一个:
- 选择 EC2 。
- 单击启动实例:
- 选择
Ubuntu Server 16.04 LTS (HVM), SSD Volume Type - ami-db710fa3:

- 选择
t2.micro实例类型:
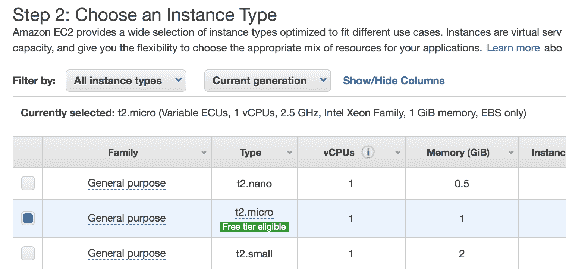
- 点击启动:

- 单击启动。
- 选择创建一个新的密钥对:
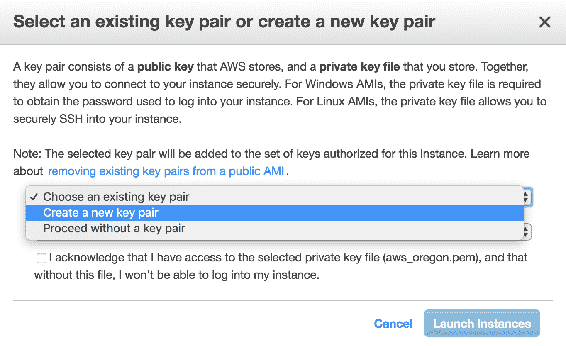
- 给它命名,然后单击启动实例。 它需要一些时间才能运行:
- 一旦其状态为
running,点击实例 ID ,在这种情况下为i-00ccaeca61a24e042。 然后选择实例并单击Connect:
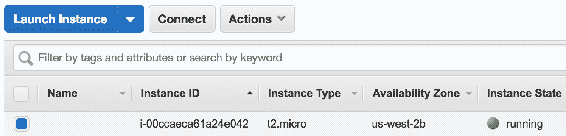
- 然后它将向您显示以下窗口,其中包含一些有用的信息:

- 打开终端,然后导航到保存所生成密钥的文件夹。 在此示例中,键名称为
aws_oregon。 运行以下命令:
$ chmod 400 aws_oregon.pem
- 然后,在上一个窗口的示例部分中复制该行并运行它:
$ ssh -i "aws_oregon.pem" ubuntu@ec2-34-219-121-1.us-west-2.compute.amazonaws.com
- 在第一个问题的答案中输入
yes将其添加到已知主机中,它将连接到您的实例:
您需要做的第一件事是通过运行以下命令来更新和升级预安装的软件包:
sudo apt-get update
sudo apt-get upgrade
sudo短语为您提供了更新和升级的必要权利,因为软件包的更改可能会对系统产生负面影响,并非所有人都可以对其进行授权。 您可以将apt-get视为 Ubuntu 的软件包管理器。
您可以创建许多虚拟环境,并链接到不同的低级库,但是,每次使用新的低级库配置 NumPy 时,您都将从一个新的预配实例开始。 这将为您提供有关配置过程的想法,以后使您可以轻松地设置虚拟环境。
安装 BLAS 和 LAPACK
为了设置您的开发环境,您需要在运行以下命令后安装所需的软件包,例如编译器,库和其他必要的部分,
$ sudo apt-get update $ sudo apt-get upgrade
对于此配置,很幸运,因为您可以运行以下命令来安装 Python 的 SciPy 软件包,它将安装所有必需的软件包,包括 NumPy,基本线性代数子程序(libblas3)和线性代数软件包(liblapack3):
$ sudo apt-get install python3-scipy
控制台输出:
- 输入
Y并按Enter继续。 安装完成后,运行以下命令以打开python3解释器:
$ python3
启动 Python 控制台:

- 导入
numpy并使用show_config方法查看 NumPy 的配置:
控制台输出:
- 由于在安装 NumPy 时可以使用 BLAS 和 LAPACK 库,因此它使用它们来构建库。 您可以在
lapack_info和blas_info中看到它们; 否则,您将不会在输出中看到它们,如以下屏幕截图所示:
- 如果您使用的是 macOS,则可以使用 Accelerate/vecLib 框架。 以下命令将输出 macOS 系统的加速器选项:
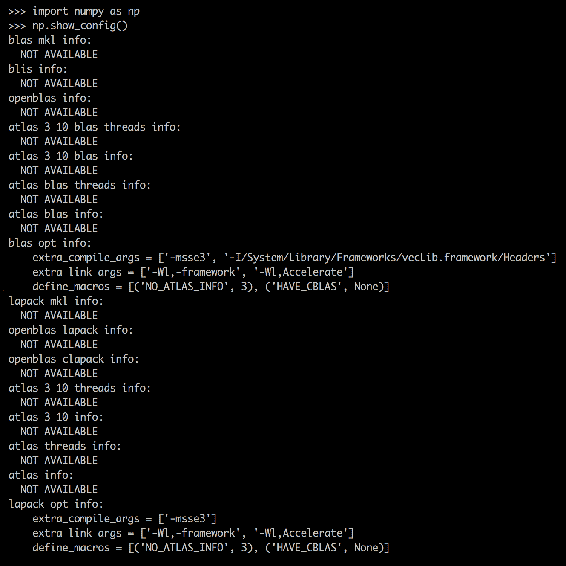
安装 OpenBLAS
OpenBLAS 的步骤略有不同,如下所示:
- 在先前的配置中运行以下命令:
$ sudo apt-get update $ sudo apt-get upgrade
- 您需要通过运行以下命令来安装
build-essential,其中包括make命令和其他必要的库:
$ sudo apt-get install build-essential libc6 gcc gfortran
- 创建一个名为
openblas_setup.sh的文件,然后粘贴以下内容。 如果您搜索 GitHub,则可以找到不同的设置脚本,并且可以尝试一种满足您需要的脚本:
##!/bin/bash
set -e
pushd /root
git clone https://github.com/xianyi/OpenBLAS.git
pushd /root/OpenBLAS
make clean
make -j4
rm -rf /root/openblas-install
make install PREFIX=/root/openblas-install
popd
ln -sf /root/openblas-install/lib/libopenblas.so /usr/lib/libblas.so
ln -sf /root/openblas-install/lib/libopenblas.so /usr/lib/libblas.so.3
ln -sf /root/openblas-install/lib/libopenblas.so /usr/lib/liblapack.so.3
- 保存此文件并运行以下命令:
$ chmod +777 openblas_setup.sh
$ sudo ./openblas_setup.sh
- 安装完成后,您可以按以下方式安装 numpy 和 scipy:
$ sudo apt-get install python3-pip
$ pip3 install numpy
$ pip3 install scipy
- 现在,您可以像以前一样检查 NumPy 配置:
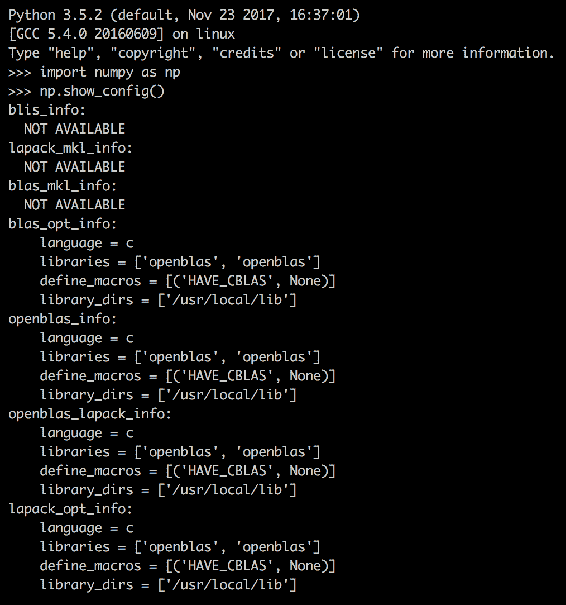
安装英特尔 MKL
为了针对英特尔 MKL 构建 NumPy 和 SciPy,请按照以下说明进行操作
- 运行以下命令:
$ sudo apt-get update
$ sudo apt-get upgrade
- 您需要安装 Anaconda 发行版,因为 Anaconda 的安装随 Intel MKL 一起提供。 首先使用以下命令下载 Anaconda:
$ wget https://repo.continuum.io/archive/Anaconda3-5.2.0-Linux-x86_64.sh
- 安装完成后,将
cd插入anaconda3/bin并运行python:
$ cd anaconda3/bin
$ ./python
- 您可以像以前一样检查
numpy配置:
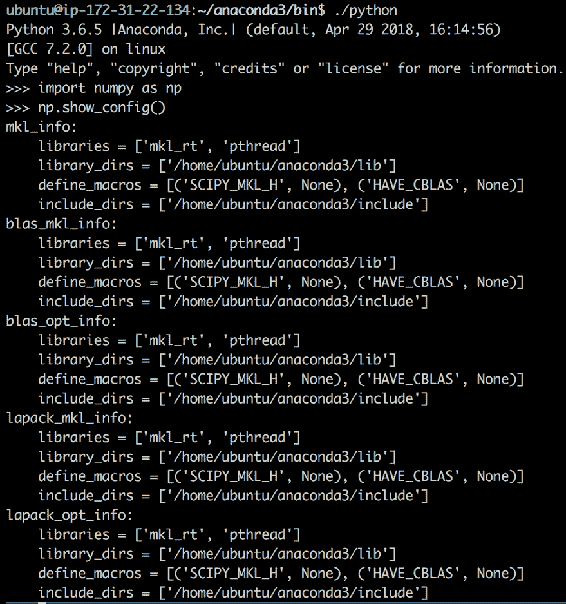
安装 ATLAS
为了针对 ATLAS 构建 NumPy,请按照以下说明进行操作
- 运行以下命令:
$ sudo apt-get update
$ sudo apt-get upgrade
- 您需要通过运行以下命令来安装
build-essential,其中包括make命令和其他必要的库:
$ sudo apt-get install build-essential libc6 gcc gfortran
- 然后,您需要安装
atlas:
$ sudo apt-get install libatlas-base-dev
- 您现在可以按以下方式安装
pip和numpy:
$ sudo apt-get install python3-pip
$ pip3 install --no-cache-dir Cython
$ git clone https://github.com/numpy/numpy.git
$ cd numpy
$ cp site.cfg.example site.cfg
$ vi site.cfg
在site.cfg内,您应注释掉地图集行,并将其设置为地图集安装,如下所示:
[atlas]
library_dirs = /usr/local/atlas/lib
include_dirs = /usr/local/atlas/include
然后运行:
$ sudo python3 setup.py install
- 安装完成后,安装
scipy:
$ pip3 install scipy
然后返回到您的主目录,启动python解释器并检查numpy配置,这将为您提供以下输出:
>>> import numpy as np
>>> np.show_config()
atlas_blas_info:
include_dirs = ['/usr/include/atlas']
language = c
library_dirs = ['/usr/lib/atlas-base']
define_macros = [('HAVE_CBLAS', None), ('ATLAS_INFO', '"\\"3.10.2\\""')]
libraries = ['f77blas', 'cblas', 'atlas', 'f77blas', 'cblas']
...
您已经介绍了上述所有低级库的配置。 是时候了解基准测试的计算密集型任务了。
用于基准测试的计算密集型任务
现在,您将能够使用不同的配置(例如是否使用 BLAS/LAPACK,OpenBLAS,ATLAS 和 Intel MKL)对 NumPy 性能进行基准测试。 让我们回顾一下要为基准计算的内容。
矩阵分解
矩阵分解或分解方法涉及计算矩阵的组成部分,以便可以使用它们简化要求更高的矩阵操作。 在实践中,这意味着将您拥有的矩阵分解为多个矩阵,这样,当您计算这些较小矩阵的乘积时,您将获得原始矩阵。 矩阵分解方法的一些示例是奇异值分解(SVD),特征值分解,Cholesky 分解,下上(LU)和 QR 分解。
奇异值分解
SVD 是线性代数中最有用的工具之一。 Beltrami 和 Jordan 发表了有关其使用的几篇论文。 SVD 用于各种应用,例如计算机视觉和信号处理。
如果您具有正方形或矩形矩阵(M),则可以将其分解为矩阵(U),矩阵(V)(计算中使用矩阵转置)和奇异值(d)。
您的最终公式将如下所示:
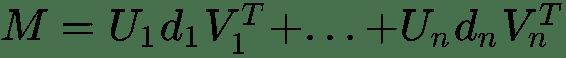
以下是奇异值分解的说明:
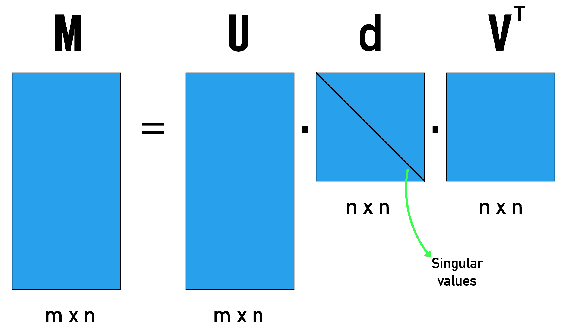
一种简单的数据精简方法是排除该公式中d小到可以忽略不计的部分。
让我们看看如何使用numpy来实现:
import numpy as np
M = np.random.randint(low=0, high=20, size=20).reshape(4,5)
print(M)
### Output
[[18 15 11 13 19]
[ 1 6 8 13 18]
[ 9 7 15 13 10]
[17 15 12 14 12]]
U, d, VT = np.linalg.svd(M)
print("U:n {}n".format(U))
print("d:n {}n".format(d))
print("VT:n {}".format(VT))
U:
[[-0.60773852 -0.22318957 0.5276743 -0.54990921]
[-0.38123886 0.86738201 0.19333528 0.25480749]
[-0.42657252 0.10181457 -0.82343563 -0.36003255]
[-0.55076919 -0.43297652 -0.07832665 0.70925987]]
d:
[56.31276456 13.15721839 8.08763849 2.51997135]
VT:
[[-0.43547429 -0.40223663 -0.40386674 -0.46371223 -0.52002929] [-0.72920427 -0.29835313 0.06197899 0.27638212 0.54682545]
[ 0.11733943 0.26412864 -0.73449806 -0.30022507 0.53557916]
[-0.32795351 0.55511623 -0.3571117 0.56067806 -0.3773643 ]
[-0.39661218 0.60932187 0.40747282 -0.55144258 0.03609177]]
### Setting full_matrices to false gives you reduced form where small values close to zero are excluded
U, d, VT = np.linalg.svd(M, full_matrices=False)
print("U:n {}n".format(U))
print("d:n {}n".format(d))
print("VT:n {}".format(VT))
### Output
U:
[[-0.60773852 -0.22318957 0.5276743 -0.54990921]
[-0.38123886 0.86738201 0.19333528 0.25480749]
[-0.42657252 0.10181457 -0.82343563 -0.36003255]
[-0.55076919 -0.43297652 -0.07832665 0.70925987]]
d:
[56.31276456 13.15721839 8.08763849 2.51997135]
VT:
[[-0.43547429 -0.40223663 -0.40386674 -0.46371223 -0.52002929]
[-0.72920427 -0.29835313 0.06197899 0.27638212 0.54682545]
[ 0.11733943 0.26412864 -0.73449806 -0.30022507 0.53557916]
[-0.32795351 0.55511623 -0.3571117 0.56067806 -0.3773643 ]]
Cholesky 分解
如果您有一个正方形矩阵,也可以应用 Cholesky 分解,将一个矩阵(M)分解为两个三角形矩阵(U和U^T)。 Cholesky 分解可帮助您简化计算复杂性。 可以将其总结为以下公式:
M = U^T U
以下是 Cholesky 分解的说明:
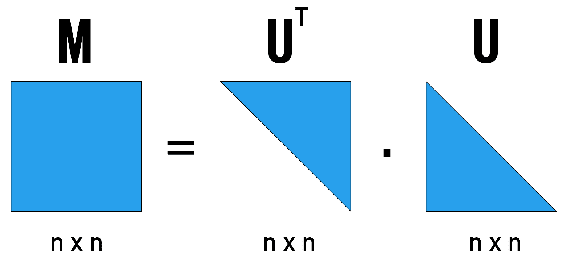
让我们看看如何使用numpy实现它:
from numpy import array
from scipy.linalg import cholesky
M = np.array([[1, 3, 4],
[2, 13, 15],
[5, 31, 33]])
print(M)
## Output
[[ 1 3 4]
[ 2 13 15]
[ 5 31 33]]
L = cholesky(M)
print(L)
### Output
[[1\. 3\. 4\. ]
[0\. 2\. 1.5 ]
[0\. 0\. 3.84057287]]
L.T.dot(L)
## Output
array([[ 1., 3., 4.],
[ 3., 13., 15.],
[ 4., 15., 33.]])
LU 分解
与 Cholesky 分解类似,LU 分解将矩阵(M)分解为下(L)和上(U)三角矩阵。 这也有助于我们简化计算密集型代数。 可以将其总结为以下公式:
M = LU
下面是 LU 分解的说明:
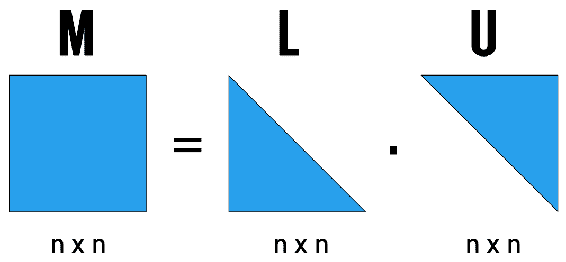
让我们看看如何使用numpy实现它:
from numpy import array
from scipy.linalg import lu
M = np.random.randint(low=0, high=20, size=25).reshape(5,5)
print(M)
## Output
[[18 12 14 15 2]
[ 4 2 12 18 3]
[ 9 19 5 16 8]
[15 19 6 16 11]
[ 1 19 2 18 17]]
P, L, U = lu(M)
print("P:n {}n".format(P))
print("L:n {}n".format(L))
print("U:n {}".format(U))
### Output
P:
[[1\. 0\. 0\. 0\. 0.]
[0\. 0\. 1\. 0\. 0.]
[0\. 0\. 0\. 0\. 1.]
[0\. 0\. 0\. 1\. 0.]
[0\. 1\. 0\. 0\. 0.]]
L:
[[ 1\. 0\. 0\. 0\. 0\. ]
[ 0.05555556 1\. 0\. 0\. 0\. ]
[ 0.22222222 -0.03636364 1\. 0\. 0\. ]
[ 0.83333333 0.49090909 -0.70149254 1\. 0\. ]
[ 0.5 0.70909091 -0.32089552 0.21279832 1\. ]]
U:
[[18\. 12\. 14\. 15\. 2\. ]
[ 0\. 18.33333333 1.22222222 17.16666667 16.88888889]
[ 0\. 0\. 8.93333333 15.29090909 3.16969697]
[ 0\. 0\. 0\. 5.79918589 3.26594301]
[ 0\. 0\. 0\. 0\. -4.65360318]]
P.dot(L).dot(U)
## Output
array([[18., 12., 14., 15., 2.],
[ 4., 2., 12., 18., 3.],
[ 9., 19., 5., 16., 8.],
[15., 19., 6., 16., 11.],
[ 1., 19., 2., 18., 17.]])
特征值分解
特征值分解也是一种适用于平方矩阵的分解技术。 使用特征值分解分解方阵(M)时,将得到三个矩阵。 这些矩阵之一(Q)在列中包含特征向量,另一个矩阵(L)在对角线中包含特征值,最后一个矩阵是特征向量矩阵(Q^(-1))。
可以将其总结为以下公式:
M = QVQ^(-1)
特征值分解将为您提供矩阵的特征值和特征向量。
下面是特征值分解的说明:

让我们看看如何使用numpy实现它:
from numpy import array
from numpy.linalg import eig
M = np.random.randint(low=0, high=20, size=25).reshape(5,5)
print(M)
## Output
[[13 9 5 0 12]
[13 6 11 8 15]
[16 17 15 12 1]
[17 8 5 7 5]
[10 6 18 5 19]]
V, Q = eig(M)
print("Eigenvalues:n {}n".format(V))
print("Eigenvectors:n {}".format(Q))
### Output
Eigenvalues:
[50.79415691 +0.j 5.76076687+11.52079216j
5.76076687-11.52079216j -1.15784533 +3.28961651j
-1.15784533 -3.28961651j]
Eigenvectors:
[[ 0.34875973+0.j -0.36831427+0.21725348j -0.36831427-0.21725348j
-0.40737336-0.19752276j -0.40737336+0.19752276j]
[ 0.46629571+0.j -0.08027011-0.03330739j -0.08027011+0.03330739j
0.58904402+0.j 0.58904402-0.j ]
[ 0.50628483+0.j 0.62334823+0.j 0.62334823-0.j
-0.27738359-0.22063552j -0.27738359+0.22063552j]
[ 0.33975886+0.j 0.14035596+0.39427693j 0.14035596-0.39427693j
0.125282 +0.46663129j 0.125282 -0.46663129j]
[ 0.53774952+0.j -0.18591079-0.45968785j -0.18591079+0.45968785j
0.20856874+0.21329768j 0.20856874-0.21329768j]]
from numpy import diag
from numpy import dot
from numpy.linalg import inv
Q.dot(diag(V)).dot(inv(Q))
## Output
array([[1.30000000e+01-2.88657986e-15j, 9.00000000e+00-2.33146835e-15j,
5.00000000e+00+2.38697950e-15j, 1.17683641e-14+1.77635684e-15j,
1.20000000e+01-4.99600361e-16j],
[1.30000000e+01-4.32986980e-15j, 6.00000000e+00-3.99680289e-15j,
1.10000000e+01+3.38618023e-15j, 8.00000000e+00+1.72084569e-15j,
1.50000000e+01-2.77555756e-16j],
[1.60000000e+01-7.21644966e-15j, 1.70000000e+01-6.66133815e-15j,
1.50000000e+01+5.71764858e-15j, 1.20000000e+01+2.99760217e-15j,
1.00000000e+00-6.66133815e-16j],
[1.70000000e+01-5.27355937e-15j, 8.00000000e+00-3.10862447e-15j,
5.00000000e+00+4.27435864e-15j, 7.00000000e+00+2.22044605e-15j,
5.00000000e+00-1.22124533e-15j],
[1.00000000e+01-3.60822483e-15j, 6.00000000e+00-4.21884749e-15j,
1.80000000e+01+2.27595720e-15j, 5.00000000e+00+1.55431223e-15j,
1.90000000e+01+3.88578059e-16j]])
QR 分解
您可以通过应用 QR 分解将正方形或矩形矩阵(M)分解为正交矩阵(Q)和上三角矩阵(R)。 可以用以下公式表示:
M = QR
以下是 QR 分解的说明:
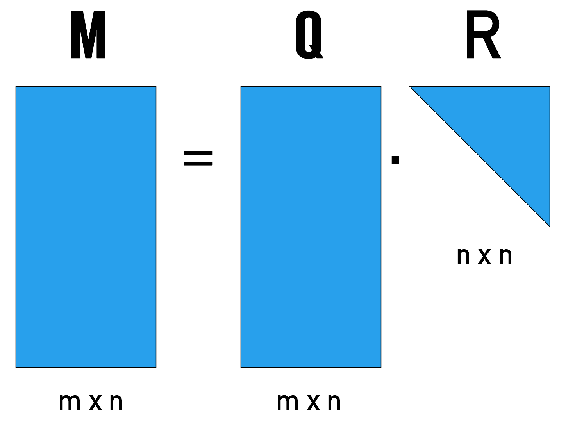
让我们看看如何使用numpy实现它:
from numpy import array
from numpy.linalg import qr
M = np.random.randint(low=0, high=20, size=20).reshape(4,5)
print(M)
## Output
[[14 6 0 19 3]
[ 9 6 17 8 8]
[ 4 13 17 4 4]
[ 0 0 2 7 11]]
Q, R = qr(M, 'complete')
print("Q:n {}n".format(Q))
print("R:n {}".format(R))
### Output
Q:
[[-0.81788873 0.28364908 -0.49345895 0.08425845]
[-0.52578561 -0.01509441 0.83834961 -0.14314877]
[-0.2336825 -0.95880935 -0.15918031 0.02718015]
[-0\. -0\. 0.16831464 0.98573332]]
R:
[[-17.11724277 -11.09991852 -12.91095786 -20.68090082 -7.59468109]
[ 0\. -10.85319349 -16.5563638 1.43333978 -3.10504542]
[ 0\. 0\. 11.88250752 -2.12744187 6.4411599 ]
[ 0\. 0\. 0\. 7.4645743 10.05937231]]
array([[1.40000000e+01, 6.00000000e+00, 1.77635684e-15, 1.90000000e+01,
3.00000000e+00],
[9.00000000e+00, 6.00000000e+00, 1.70000000e+01, 8.00000000e+00,
8.00000000e+00],
[4.00000000e+00, 1.30000000e+01, 1.70000000e+01, 4.00000000e+00,
4.00000000e+00],
[0.00000000e+00, 0.00000000e+00, 2.00000000e+00, 7.00000000e+00,
1.10000000e+01]])
处理稀疏线性系统
您将不会总是使用密集矩阵,并且当您需要使用稀疏矩阵时,有些库将帮助您优化稀疏矩阵运算。 即使这些可能没有 Python API,您仍可能需要通过使用其他编程语言来使用它们,例如 C 和 C++:
- Hypre:包含预处理器和求解器,以利用并行实现来处理稀疏线性方程组。
- SuperLU:处理大型,稀疏,不对称的线性方程组。
- UMFPACK:解决稀疏线性方程组。
- CUSP:带有并行实现的稀疏线性代数和图形计算的开源库。 通过使用 CUSP,您可以访问 NVIDIA GPU 提供的计算资源。
- cuSPARSE:包含用于处理稀疏矩阵的线性代数子例程。 与 CUSP 一样,您可以访问 Nvidia GPU 提供的计算资源。
总结
在本章中,您探索了可以与 NumPy 配对的各种低级库及其配置。 我们特意运行了 EC2 条款,以便您熟悉基本的 Linux 命令行操作。 您还研究了各种计算密集型,数值,线性代数运算,这些运算将在下一章中用作基准测试不同的配置。
在下一章中,我们将创建一个基准 python 脚本,以在每种配置上运行。 您将能够查看不同线性代数运算和不同矩阵大小的性能指标
九、性能基准
在本章中,您将研究上一章介绍的不同配置的性能统计信息。 当然,当前设置无法为您提供最准确的环境,因为您无法控制 EC2 实例,但是它将使您了解自己环境中所需的设置。
我们将涵盖以下主题:
- 基准的重要性
- BLAS,LAPACK,OpenBLAS,ATLAS 和 Intel MKL 的性能
- 最终结果
为什么我们需要基准?
随着编程技巧的提高,您将开始实施更高效的程序。 您将搜索数十个代码存储库,以了解其他人如何解决类似的问题,并且您会发现那些令您赞叹不已的稀有宝石。
在编写更好的软件和实施系统的整个过程中,您将需要测量和跟踪改进速度的方法。 通常,您将以起点为基准,并查看所做的改进将如何累加性能指标。
设置基准后,您将对几种不同的实现进行基准测试,并将有机会根据您选择的性能指标进行比较。 您可以选择各种指标,并且需要事先决定。
这些基准的性能指标将保持相当简单,并且仅使用所花费的时间指标。 您将使用不同的配置多次执行相同的操作,并首先计算平均花费的时间。 计算平均值的公式为:
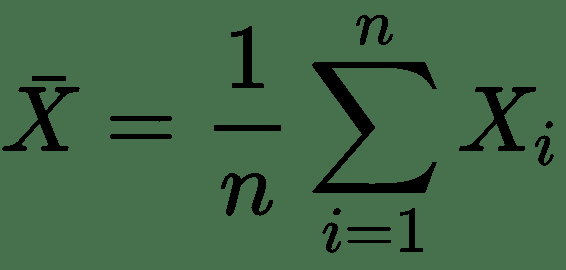
这是一个计算均值的好公式; 在我们的示例中,公式解释如下:
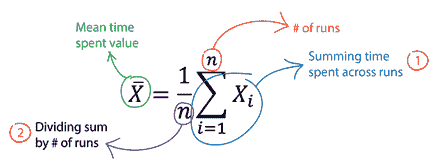
基线将基于此公式创建。 第一组计算如下:
的加法和乘法:
- 向量向量
- 向量矩阵
- 矩阵矩阵
通常,您将运行这些计算给定次数并计算平均值。
以下代码段向您展示了一个自定义函数,而不是 Python 中可用的通用计时器。 使用自定义函数的原因是,您以后可以将其与其他统计函数一起扩展,并通过适当的日志记录更好地查看详细信息。 函数将在计算开始之前输出有用的信息,并在迭代完成之后输出结果。
import inspect
import time
from datetime import datetime
def timer(*args, operation, n):
"""
Returns average time spent
for given operation and arguments.
Parameters
----------
*args: list (of numpy.ndarray, numpy.matrixlib.defmatrix.matrix or both)
one or more numpy vectors or matrices
operation: function
numpy or scipy operation to be applied to given arguments
n: int
number of iterations to apply given operation
Returns
-------
avg_time_spent: double
Average time spent to apply given operation
std_time_spent: double
Standard deviation of time spent to apply given operation
Examples
--------
>>> import numpy as np
>>> vec1 = np.array(np.random.rand(1000))
>>> vec2 = np.array(np.random.rand(1000))
>>> args = (vec1, vec2)
>>> timer(*args, operation=np.dot, n=1000000)
8.942582607269287e-07
"""
# Following list will hold the
# time spent value for each iteration
time_spent = []
# Configuration info
print("""
-------------------------------------------
### {} Operation ###
Arguments Info
--------------
args[0] Dimension: {},
args[0] Shape: {},
args[0] Length: {}
""".format(operation.__name__,
args[0].ndim,
args[0].shape,
len(args[0])))
# If *args length is greater than 1,
# print out the info for second argument
args_len = 0
for i, arg in enumerate(args):
args_len += 1
if args_len > 1:
print("""
args[1] Dimension: {},
args[1] Shape: {},
args[1] Length: {}
""".format(args[1].ndim,
args[1].shape,
len(args[1])))
print("""
Operation Info
--------------
Name: {},
Docstring: {}
Iterations Info
---------------
# of iterations: {}""".format(
operation.__name__,
operation.__doc__[:100] +
"... For more info type 'operation?'",
n))
print("""
-> Starting {} of iterations at: {}""".format(n, datetime.now()))
if args_len > 1:
for i in range(n):
start = time.time()
operation(args[0], args[1])
time_spent.append(time.time()-start)
else:
for i in range(n):
start = time.time()
operation(args[0])
time_spent.append(time.time()-start)
avg_time_spent = np.sum(time_spent) / n
print("""
-> Average time spent: {} seconds,
-------------------------------------------
""".format(avg_time_spent))
return avg_time_spent
当此函数中包含Docstring时,可以显示它以查看函数参数,返回的内容以及用法示例:
print(timer.__doc__)
这将生成以下输出:
Returns average time spent
for given operation and arguments.
Parameters
----------
*args: list (of numpy.ndarray, numpy.matrixlib.defmatrix.matrix or both)
one or more numpy vectors or matrices
operation: function
numpy or scipy operation to be applied to given arguments
n: int
number of iterations to apply given operation
Returns
-------
avg_time_spent: double
Average time spent to apply given operation
Examples
--------
>>> import numpy as np
>>> vec1 = np.array(np.random.rand(1000))
>>> vec2 = np.array(np.random.rand(1000))
>>> args = [vec1, vec2]
>>> timer(*args, operation=np.dot, n=1000000)
8.942582607269287e-07
让我们开始测量两个向量的点积所花费的平均时间。 以下代码块定义向量,并创建要输入到计时器函数中的参数:
import numpy as np
vec1 = np.array(np.random.rand(1000))
vec2 = np.array(np.random.rand(1000))
args = [vec1, vec2]
您现在可以按以下方式调用计时器函数:
timer(*args, operation=np.dot, n=1000000)
-------------------------------------------
### dot Operation ###
Arguments Info
--------------
args[0] Dimension: 1,
args[0] Shape: (1000,),
args[0] Length: 1000
args[1] Dimension: 1,
args[1] Shape: (1000,),
args[1] Length: 1000
Operation Info
--------------
Name: dot,
Docstring: dot(a, b, out=None)
Dot product of two arrays. Specifically,
- If both `a` and `b` are 1-D... For more info type 'operation?'
Iterations Info
---------------
# of iterations: 1000000
-> Starting 1000000 of iterations at: 2018-06-09 21:02:51.711211
-> Average time spent: 1.0054986476898194e-06 seconds,
-------------------------------------------
1.0054986476898194e-06
我们的向量乘积平均需要 1 微秒。 让我们看看如何通过添加其他指标来改进此计算。 您可以轻松添加的另一个指标是标准差,如下公式所示:
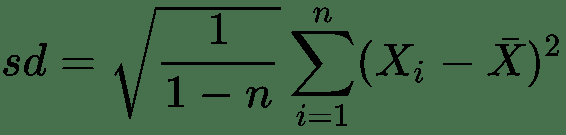
您熟悉上图中的公式术语。 标准差只是告诉您所报告指标的可变性,这是在我们的示例中花费的平均时间。
通过计算std_time_spent,打印其值并返回以下内容来扩展计时器函数:
avg_time_spent = np.sum(time_spent) / n
std_time_spent = np.std(time_spent)
print("""
-> Average time spent: {} seconds,
-> Std. deviation time spent: {} seconds
""".format(avg_time_spent, std_time_spent))
return avg_time_spent, std_time_spent
您还可以如下更新Docstring:
Returns
-------
avg_time_spent: double
Average time spent to apply given operation
std_time_spent: double
Standard deviation of time spent to apply given operation.
您可以重新定义时间函数,然后再次运行先前的计算,如下所示:
timer(*args, operation=np.dot, n=1000000)
您将获得以下输出(为简洁起见,仅显示最后一部分)以及其他信息:
-> Starting {} of iterations at: {}".format(n, datetime.now())
-> Average time spent: 1.0006928443908692e-06 seconds,
-> Std. deviation time spent: 1.2182541822530471e-06 seconds
(1.0006928443908692e-06, 1.2182541822530471e-06)
大! 您还添加了哪些其他指标? 如何添加置信区间? 该部分将留给您锻炼,但是对您来说应该很容易!
让我们继续向量矩阵乘积:
mat1 = np.random.rand(1000,1000)
args = [vec1, mat1]
timer(*args, operation=np.dot, n=1000000)
这将为您提供以下输出:
Arguments Info
--------------
args[0] Dimension: 1,
args[0] Shape: (1000,),
args[0] Length: 1000
args[1] Dimension: 2,
args[1] Shape: (1000, 1000),
args[1] Length: 1000
Operation Info
--------------
Name: dot,
Docstring: dot(a, b, out=None)
Dot product of two arrays. Specifically,
- If both `a` and `b` are 1-D... For more info type 'operation?'
Iterations Info
---------------
# of iterations: 1000000
-> Starting 1000000 of iterations at: 2018-06-09 19:13:07.013949
-> Average time spent: 0.00020063393139839174 seconds,
-> Std. deviation time spent: 9.579314466482879e-05 seconds
(0.00020063393139839174, 9.579314466482879e-05)
最后,矩阵矩阵乘法如下:
mat1 = np.random.rand(100,100)
mat2 = np.random.rand(100,100)
args = [mat1, mat2]
timer(*args, operation=np.dot, n=1000000)
这将为您提供类似于先前输出的输出。
现在,我们或多或少有了一个想法,即如何挑战如何在计算机上执行这些任务。 基准函数列表已完成,在上一章中您看到了将点积添加到矩阵分解中的信息。
您将要做的是创建一个包含这些计算和统计信息的 Python 脚本文件。 然后,您将使用在 AWS 上设置的不同配置运行此文件。
让我们看一下linalg_benchmark.py,您可以在这个页面 中找到它。
以下代码块向您展示了linalg_benchmark.py脚本的重要部分,该脚本将用于测试您先前在 AWS 上设置的不同配置:
## Seed for reproducibility
np.random.seed(8053)
dim = 100
n = 10000
v1, v2 = np.array(rand(dim)), np.array(rand(dim))
m1, m2 = rand(dim, dim), rand(dim, dim)
## Vector - Vector Product
args = [v1, v2]
timer(*args, operation=np.dot, n=n)
## Vector - Matrix Product
args = [v1, m1]
timer(*args, operation=np.dot, n=n)
## Matrix - Matrix Product
args = [m1, m2]
timer(*args, operation=np.dot, n=n)
## Singular-value Decomposition
args = [m1]
timer(*args, operation=np.linalg.svd, n=n)
## LU Decomposition
args = [m1]
timer(*args, operation=lu, n=n)
## QR Decomposition
args = [m1]
timer(*args, operation=qr, n=n)
## Cholesky Decomposition
M = np.array([[1, 3, 4],
[2, 13, 15],
[5, 31, 33]])
args = [M]
timer(*args, operation=cholesky, n=n)
## Eigenvalue Decomposition
args = [m1]
timer(*args, operation=eig, n=n)
print("""
NumPy Configuration:
--------------------
""")
np.__config__.show()
将有两个单独的运行:
- 1 st 与
dim = 100一起运行 - 2 和与
dim = 500一起运行
让我们看一下结果。
准备性能基准
对于每个实例和配置,导航到您的Home目录并创建一个名为py_scripts的文件夹:
使用以下命令创建名为linalg_benchmark.py的文件并粘贴内容:
粘贴内容后,键入:,然后键入wq!和Enter保存并退出:
现在,您可以使用以下命令运行该文件:
对于 Anaconda 分发,您将使用以下命令运行脚本:
BLAS 和 LAPACK 的性能
在这里,您将使用 BLAS 和 LAPACK 运行linalg_benchmark.py脚本。 连接到具有此配置的t2.micro实例,然后如上一节中所示运行脚本。
以下是dim = 100的运行结果:
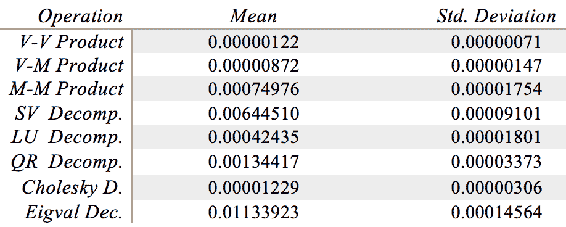
以下是dim = 500的运行结果:
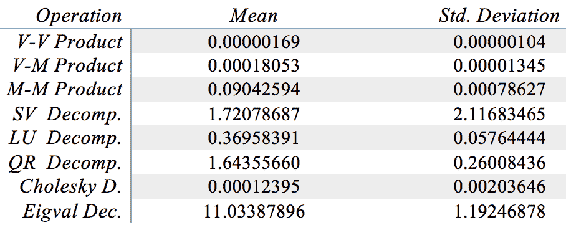
OpenBLAS 的性能
在这里,您将使用 OpenBLAS 运行linalg_benchmark.py脚本。 连接到具有此配置的t2.micro实例,然后运行上一节中显示的脚本。
以下是dim = 100的运行结果:

以下是dim = 500的运行结果:
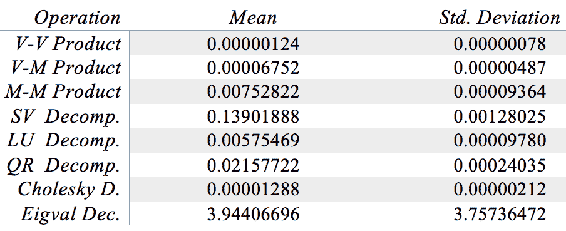
ATLAS 的性能
在这里,您将使用 ATLAS 运行linalg_benchmark.py脚本。 连接到具有此配置的t2.micro实例,如上一节中所示运行脚本。
以下是dim = 100的运行结果:
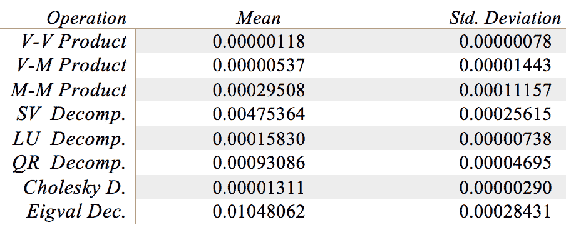
以下是dim = 500的运行结果:
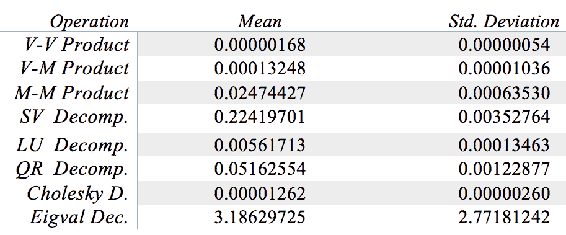
英特尔 MKL 的性能
在这里,您将使用英特尔 MKL 运行linalg_benchmark.py脚本。 连接到具有此配置的t2.micro实例,然后运行上一节中显示的脚本。
以下是dim = 100的运行结果:
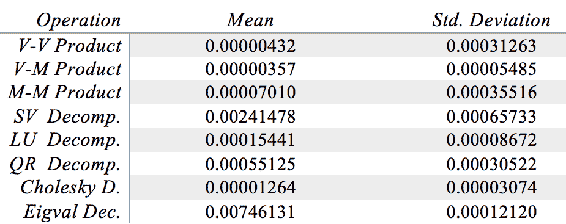
以下是dim = 500的运行结果:
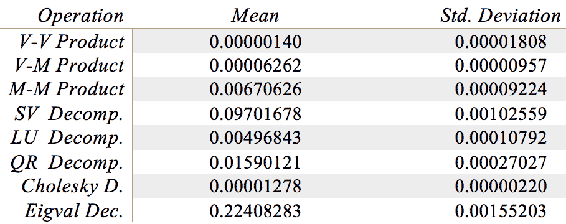
结果
当然,t2.micro实例相当薄弱,您应该更多地了解 Amazon 如何为 EC2 实例提供这种计算能力。 您可以在这个页面 上阅读有关它们的更多信息。
如果您使用功能更强大的计算机并具有更多的内核,则不同配置之间的性能差异将更加明显。
说到结果,毫不奇怪,默认安装的 BLAS 和 LAPACK 为我们提供了基准性能,而经过优化的版本(如 OpenBLAS,ATLAS 和 Intel MKL)提供了更好的性能。
正如您已经指出的那样,您没有在 Python 脚本中更改任何代码行,而仅通过将 NumPy 库与不同的加速器链接起来,便获得了巨大的性能提升。
如果您将更深入地研究这些低级库以了解提供了哪些特定的例程和函数,则将更好地了解程序的哪些部分将从这些实现中受益。
当然,起初您可能还不了解许多其他细节。 可能是您使用的函数未使用低级库或未并行化操作的情况。 在某些情况下,多线程会或不会有所帮助。 知识和经验最终取决于您的实验,并且您将从自己的经验中学到东西,因此您将更加精通各种应用。
许多研究人员发表了实验的设计和结果。 Google 的快速搜索将为您提供大量资源,以阅读和了解这些库在不同硬件和软件配置下的性能。
总结
在本章中,您探讨了执行计算密集型线性代数运算时不同配置的性能。
基准测试是一项严肃的工作,您至少现在已经具备运行基准测试的基本技能。 您在本章中学习的材料远未完成,但是它为您提供了从哪里开始的想法,并且您肯定可以在许多方面进行改进。
您可以看到的一件事是,逐渐增加向量和矩阵的大小时性能指标的行为。 理想情况下,您将需要功能更强大的硬件,但是t2.micro实例在大多数情况下是免费的,或者提供的价格非常便宜。
由于您将需要处理更多的计算密集型工作负载,因此重要的是要了解您的选择以及哪种选择将为您带来最佳性能。 您可以运行这些简单的实验,至少对性能有所了解,这将为您带来很多帮助,并节省时间和金钱。
如果您走了这么远,恭喜! 我们认为,遍历所有章节并学习相关材料可以提高您在 Python 科学堆栈方面的技能。